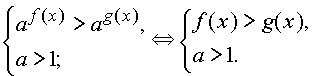
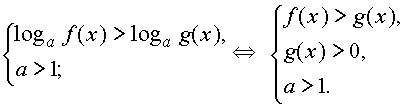
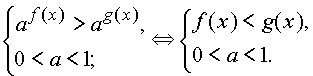
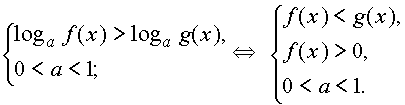
@Решение
логарифмических и показательных неравенств во многих случаях может быть
сведено к решению следующих неравенств
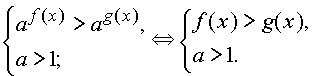 |
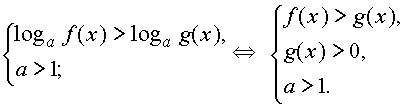 |
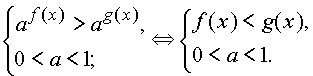 |
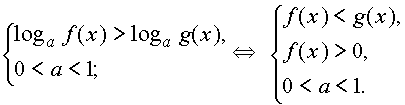 |
Более сложные неравенства сводятся к неравенствам указанного вида методами, аналогичными применяемым при решении показательных и логарифмических уравнений.
|
|
|
||
|
|
|
||
|
|
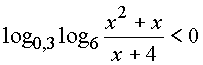 |
|
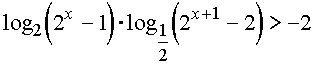 |
|
|
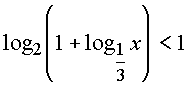 |
||
| @ | При решении неравенств вида | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| обычно следуют следующей схеме: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. Находят ОДЗ неравенства, исходя из того, что на ОДЗ функции f(x) и g(x) определены и положительны | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. Логарифмируют неравенство, т.е. заменяют неравенство равносильным ему на ОДЗ при a > 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| неравенством | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. Решают полученное неравенство. Его решения и будут решениями исходного неравенства | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| @ | При решении неравенств вида | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| обычно
следуют схеме:
1. Находят ОДЗ неравенства, исходя из того, что f(x), g(x), j (x),y (x) на ОДЗ определены, положительны и j (x)№1,y (x)№1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.
Переходят в логарифмах к некоторому основанию a,
где a>0, a№1т.е.
заменяют неравенство
равносильным ему на ОДЗ неравенством |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
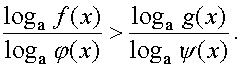 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (Отметим, что ОДЗ последнего и исходного неравенств совпадают.) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. Решают полученное неравенство. Его решения и будут решениями исходного неравенства. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сформулируем ещё несколько утверждений, часто использующихся
при решении неравенств:
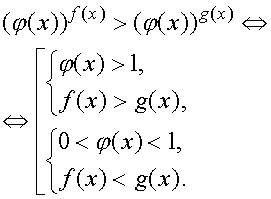 |
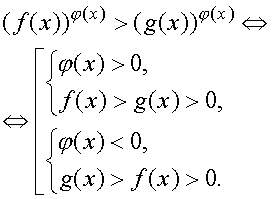 |
| Неравенство
или |
Неравенство
или |
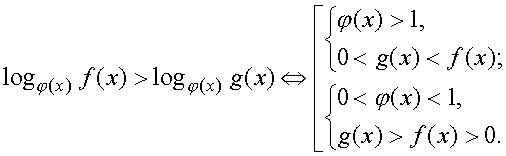 |
|
|
|
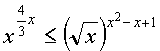 |
|
|
|
|
|
|
|
|
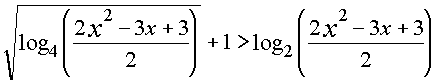 |
|
|