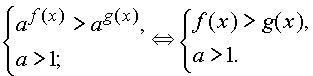
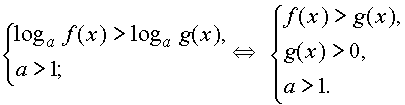
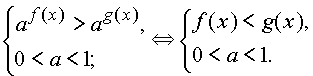
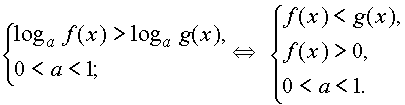
3.4. Показательные и логарифмические неравенства
Решение логарифмических и показательных неравенств во многих случаях может быть сведено к решению следующих неравенств
|
|
|
|
|
|
Решение нестрогих неравенств отличается от решения соответствующих строгих неравенств включением в множество всех решений множества корней соответствующих уравнений.
Более сложные неравенства сводятся к неравенствам указанного вида методами, аналогичными применяемым при решении показательных и логарифмических уравнений.
Пример
3.4.1. (КубГУ, матем., устн. экз.). Решить неравенство![]() .
.
Решение
|
Пусть |
|
Тогда после простейших преобразований получаем |
|
|
||
Откуда, возвращаясь к переменной
x и логарифмируя, имеем:![]()
|
Ответ: |
|