Пример
3.4.6. (КубГУ, матем., 1980 г.). Решить неравенство![]()
Решение
Неравенство равносильно системе
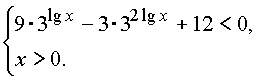
|
Пусть |
|
тогда y > 0, |
|
и первое неравенство |
||
|
системы принимает вид |
|
или, раскладывая |
||||
|
квадратный трехчлен на множители, |
|
|||||
Применяя к последнему неравенству метод интервалов,
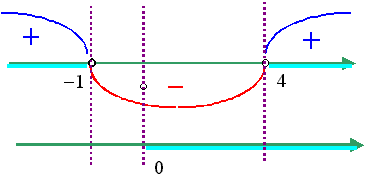
видим, что его решениями, удовлетворяющими условию
y > 0 будут все y > 4.Таким образом исходное неравенство эквивалентно системе:
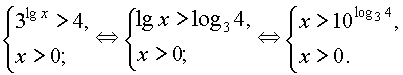
|
Итак, решениями неравенства являются все |
|
|
Ответ: |
|