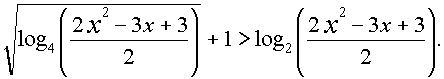
Пример
3.4.11. (КубГУ, ФПМ, 1989 г.). Решить неравенство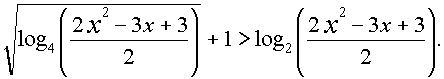
Решение
Так как 2
x2 - 3x + 3 > 0 при всех действительных x, то неравенство равносильно системе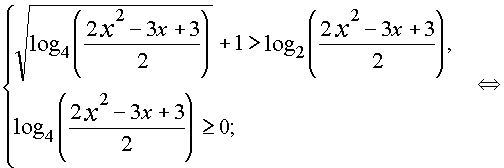
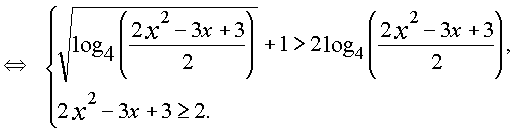
Для решения второго неравенства воспользуемся методом интервалов

![]()
В первом неравенстве сделаем замену
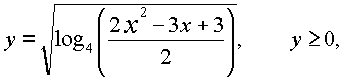
тогда приходим к неравенству 2y
2 - y - 1 < 0 и, применив метод интервалов, получаем, что решениями будут те y, которые удовлетворяют неравенству -0,5 < y < 1.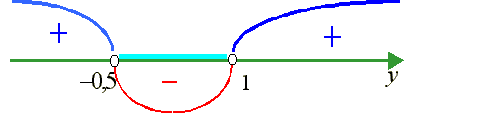
![]()
|
Откуда, так как |
|
получаем неравенство |
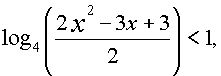
которое выполняется при тех
x, для которых 2x2 - 3x - 5 < 0. Вновь применим метод интервалов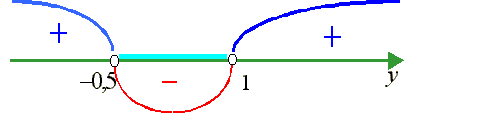
![]()
Теперь с учетом решения второго неравенства системы окончательно получаем
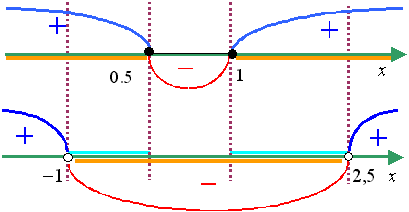
![]()
|
Ответ: |
|