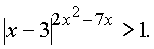
Пример
3.4.9. (КубГУ, матем., 1979 г.). Решить неравенство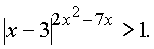
Решение
1-й
способ. ОДЗ определяется неравенством x № 3. Логарифмируя при таких x по основанию 10, получаем![]()
Последнее неравенство можно было бы решать применяя правила разложения, т.е. сравнивая с нулём сомножители. Однако в данном случае легко определить интервалы знакопостоянства функции
![]()
поэтому можно применить метод интервалов.
Функция
f(x) = 2x(x - 3,5)lg| x - 3| непрерывна при x № 3 и обращается в ноль в точках x1 = 0, x2 = 3,5, x3 = 2, x4 = 4. Таким образом (см. примеры использования метода интервалов в начале параграфа), определяем интервалы знакопостоянства функции f(x):|
|
|
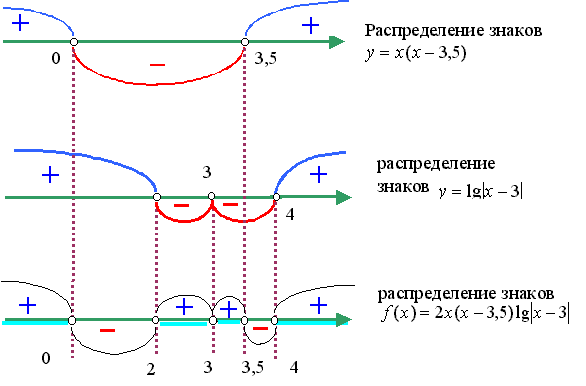
|
Ответ: |
|
2-й способ
. Применим непосредственно к исходному неравенству идеи метода интервалов.Для этого напомним, что выражения
ab - ac и (a - 1)(b - 1) имеют один знак. Тогда наше неравенство при x № 3 равносильно неравенству|
|
или |
|
Поcледнее неравенство решается методом интервалов

|
Ответ: |
|