*Заочная математическая школа

8-й класс (3-я часть)

Составители: доценты КубГУ  Сергеев Э.А. и Титов Г.Н.

 

Тема7. Неравенства.

Для любых чисел а и b следующее неравенства равно-сильны: а<b, b>a, a–b<0 и b–a>0. Также равносильны неравенства: а£b, b³a, a–b£0 и b–a³0. Часто для доказательства равенства чисел используют признак: если а£b и b£а , то а=b. Отметим наиболее часто применяемые при решении задач свойства числовых неравенств: для любых чисел а, b, с и d имеем: 1) из а£b  и b£с следует а£с; 2) а£b равносильно а+с£b+с; 3) а£b равносильно а×с£b×с при положительном с; 4) а£b равносильно b×с£а×с при отрицатель-ном с; 5) из а£b и с£d  следует а+с£b+d  и а–d£b–с; 6) из а£b и c£d следует a×c£b×d и a/d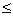b/c при положительных a, b, c, d.

Во всех приведенных свойствах 1)-6) вместо знака “£ ” можно поставить знак “<”.

 

Пример 1 (неравенство Коши).

Доказать, что (a+b)/2  для любых неотрицательных чисел а и b, причем  лишь при а=b.

 

Решение. Так как квадрат числа является неотрицательным, то . Откуда . По свойству 2), прибавляя к обеим частям , получаем равносильное неравенство , откуда по свойству 3), умножая обе части на , окончательно получаем . Теперь замечаем, что равенство возможно лишь при ,т.е.а=b.

 

Задача 1. Пусть . а) Найти наименьшее значение суммы a+b, если a×b=100. б) Найти наибольшее значение произведения a×b, если a+b=100.

 

Указание: можно использовать неравенство Коши.

 

Задача 2. Докажите для любых чисел a и b:

а) ;   б) .

Полезным является следующее свойство числовых неравенств: 7) a<b равносильно  для любых  и натуральных n.

 

Пример 2. Сравните числа: а)и;б)и.

Решение. а)  и . Так как 125<243, то по свойству 7)  и поэтому .

б) По свойству 7) достаточно сравнить квадраты этих чисел.  и . Допустим * - какой-то знак неравенства и . Это неравенство согласно свойству 2) (к обеим частям прибавили по (–5)) равносильно , которое согласно свойству 7) равносильно , т.е. 24*25. Откуда получаем, что * - это будет знак “<“ и окончательно получаем .

 

Задача 3. Сравните числа: а)и;б)и .

 

Довольно часто в олимпиадных задачах встречаются неравенства с целыми числами. Поэтому полезным является свойство: 8) a<b равносильно  для целых чисел a и b.

 

Задача 4. В торговой лавке Карабаса продаются за рубли черепашки и пиявки, причем 42 пиявки стоят дороже 35, но дешевле 36 черепашек. Сможет ли Буратино, имея 100 рублей, купить 8 черепашек?

 

Указание: если m руб.- цена пиявки и n руб.- цена черепашки (m,n - натуральные числа),то можно получить  и , откуда  (докажите).

 

Задача 5. а) Докажите, что в треугольнике сумма длин двух медиан меньше его периметра. б) Докажите, что если a, b и c - длины сторон треугольника, то справедливо неравенство .

 

Тема8.Квадратные радикалы и уравнения.

Знак “” арифметического корня из неотрицательного числа еще называют квадратным радикалом. Для любого числа a имеем , а для любых неотрицательных чисел a и b равенства , a=b,  равносильны.

 

Задача 6.а) Доказать тождество Евклида при  и :

.

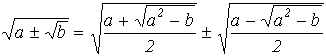Упростите выражения:

б) ;       в) ;  г) .

 

Указание:  а) достаточно убедиться, что левая и правая части при указанных a и b будут неотрицательными, а затем возвести обе части в квадрат; б) можно использовать тождество Евклида; в)-г)подкоренное вы-ражение представить в виде квадрата  разности  чисел.

Для решения следующих задач необходимо изучить соответствующий материал учебника по алгебре (8-й класс, под ред. С.А.Теляковского).

Квадратный трехчлен   при-надлежит к основному классу функций школьной матема-тики. С ним связаны следующие тождества и формулы:

(1)  ;

(2)  ;

(3)   и , где - дискриминант, - корни трехчлена при . Формулы (3) называют формулами Виета (выучите формулировку прямой и обратной теоремы Виета). Они позволяют, не находя корней квадратного трехчлена, по одним коэффициентам вычислить симметрические выражения его корней, например, такие: , , 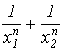,  и т.п..

Пример 3. Не находя корней уравнения , где  и , вычислить  при n=3.

Решение. Так как

, в силу  и  получаем . Поэтому мы можем вычислять  при n=3;4;5;..., учитывая  и .

В частности, .

 

Задача 7. а) Вычислить  для k=4;5;6, где - корни уравнения .  б) Не решая уравнения , и считая, что - его корни, составьте какое-нибудь новое квадратное уравнение, корни которого равны 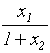 и .

 

Пример 4. Найти все значения а, при которых уравнение  имеет только целые корни.

Решение. Полагая, что - целые корни данного уравнения, по формулам (3) имеем  и . Пусть для определенности . Тогда возможны случаи:  и , а значит ;  и , а значит а=-1; x₁=-3, x₂=2, тогда a=1; x₁=-6, x₂=1, тогда a=5 . Ответ: –5; –1; 1; 5.

 

Задача 8. Найти все значения а, при которых уравнение  имеет только целые корни.

 

Из теоремы Виета следует: для того, чтобы квадратный трехчлен   имел корни одного знака, необходимо и достаточно, чтобы были выполнены следующие условия:  и ; при этом оба корня положительны, если , и отрицательны, если . Для того, чтобы квадратный трехчлен имел корни разных знаков, необходимо и достаточно выполнение условия: .

 

Задача 9. Найти все значения а, для которых уравнение  имеет:  а) отрицательные корни; б) положительные корни;  в) корни разных знаков.

 

 

Тема9. Начала тригонометрии.

Перед решением задач необходимо ознакомиться, например, с содержанием §7 в учебнике по геометрии А.В. Погорелова или §7 в учебнике по геометрии И.Ф. Шарыгина. Для закрепления указанного материала предлагается следующая задача.

 

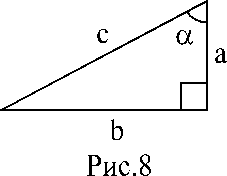
Задача 10. Согласно рисунку решите каждое из следующих заданий:

а) дано: а, a; найти b, c; 

б) дано: c, a; найти a, b;

в) дано: c=2a; найти a;

г) дано: , b=3; найти c, a;

д) используя равенства:

 (Теорема Пифагора), , ,  и , докажите 

(1) ;  (2) ;    (3)  ;

(4) ; (5) ; (6)  .

 

Для решения следующих задач желательно ознакомиться с материалом из §12 в учебнике А.В Погорелова или из §7.2 в учебнике И.Ф. Шарыгина. Задачи 11-13 представляют собой известные теоремы планиметрии.

 

Задача 11(Теорема синусов). а) Докажите, что в любом треугольнике отношение длины стороны к синусу противолежащего ей угла равно диаметру окружности, описанной около треугольника. б) Докажите для произвольного треугольника АВС справедливость равенств:      .

 

Указание: а) около треугольника АВС опишем окружность с центром О. Прямая АО пересечет окружность еще в точке D. Тогда AD - диаметр, ÐADB=ÐACD (почему?), а треугольник ABD является прямоугольным (почему?),откудаи т.д.;б) следует из а).

 

Задача 12(Теорема о биссектрисе). Пусть AL-биссектриса угла А треугольника АВС. Докажите, что BL/CL=AB/AC. 

 

Указание: полагая ÐBAL=ÐCAL=a, ÐALB=b и, учитывая sinÐALC=sin(180°–b)=sinb(почему ?), по теореме синусов для треугольника ABL имеем , а для треугольника ACL имеем:  и т.д..

 

Задача 13 (Теорема косинусов). Для любого треугольника 

АВС докажите .

 

Указание. Допустим, угол С является острым и AD- высота треугольника АВС (точка D принадлежит прямой ВС). В прямоугольном треугольнике ACD находим АС×sinÐC=AD и АС×cosÐC=CD, а значит,

 BD=½ВС-АС·cosÐC½. Применяя теорему Пифагора в прямо-угольном треугольнике ABD, после преобразований получим требуемое равенство (сделать  самостоятельно). Когда угол С не менее 90°, рассуждаем аналогично.

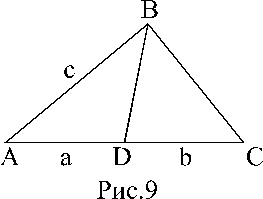
Пример 5. В треугольнике ABC точка D лежит на стороне АС (см. рис). Известно, что АВ=с, ВС=d,   

AD=a и CD=b. Найдите BD.

Решение. В треугольнике АВС обозначим угол А через a.  Тогда по теореме косинусов, учитывая АС=a+b, получим

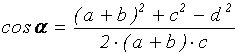. Откуда после преобразований найдем: . Таким образом, в треугольнике ABD нам будут известны две стороны АВ=с и AD=a, а также косинус угла между ними. Поэтому, применяя еще раз теорему косинусов для треугольника ABD, находим:

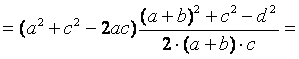
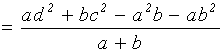. Откуда окончательно получаем ответ: .

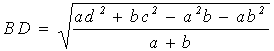Задача 14. В треугольнике АВС известно, что АВ=4 см., ВС=5 см и АС=6 см, точки H, M и L лежат на стороне АС, причем BH - высота, BM - медиана и BL - биссектриса треугольника АВС. а) Определить, является ли треугольник АВС прямоугольным, остроугольным или тупоугольным; б) найти BH;  в) найти BM; г) найти BL.

 

Указание:

а) достаточно найти косинус наибольшего угла с учетом, что косинус прямого угла равен нулю, острого угла – больше нуля и тупого угла – меньше нуля;

б) сначала можно найти косинус угла А, а затем в прямоугольном треугольнике ABH найти BH; 

в) зная, что АМ=МС=3 см., и определив косинус угла А в задании б), решаем это задание по аналогии с решением примера 5; 

г) применяя теорему о биссектрисе, можно определить длины отрезков AL и CL, а далее рассуждаем, как и в примере 5.