Тема 5. Простые числа.

 

Если натуральное число m является составным, то для наименьшего простого делителя  p  числа  m выполняется неравенство . В частности, если для любого простого числа q такого, что  число q не делит нацело натуральное число n (n>1), то n - простое число.

 

ЗАДАЧА 1. Не используя таблицу простых чисел, покажите, что 1997 - простое число.

 

Простых чисел существует бесконечно много. Действительно, предполагая противное, то есть числа   для некоторого натурального n являются всеми простыми числами, тогда согласно основной теореме арифметики число  должно делиться на какое-то простое число p, которое в силу предположения будет одним из чисел . Откуда  должно делиться на p, что невозмжно. Противоречие и означает, что множество простых чисел бесконечно (это доказательство принадлежит Евклиду). Особую трудность представляют задачи, в которых требуется найти простые числа заданного вида. Оказывается, что существует бесконечно много простых чисел вида а+b×n, где a и b - фиксированные взаимно простые натуральные числа, а n - произвольное натуральное число (теорема Дирихле). Например, при натуральных числах n существует бесконечно много простых чисел вида 1996+1997×n. До сих пор неизвестно: является ли множество натуральных чисел вида  (числа Ферма) или вида  (числа Мерсенна) конечными или нет?

УПРАЖНЕНИЕ 1. а) Найдите все простые числа p, чтобы p-28 и p+40 тоже были простыми. б) Докажите, что остаток при делении любого простого числа на 30 не является составным числом.

Решение. а) Так как  и , то числа , p и p+40 имеют разные остатки при делении на 3. Поэтому, хотя бы одно из них делится на 3 и в силу простоты равно 3. Так как  - наименьшее из них, то =3 и тогда p=31 и  p+40=71 тоже простые числа.

Ответ: p=31.

б) Для простого p имеем p=30q+r, где q - частное при делении на 30, а r - остаток, т.е. r<30. Если r - составное число, то легко проверить, что d=НОД(r;30)¹1. Поэтому  d делит нацело 30×q+r, равное p. Но p - простое и d¹1, откуда d=p и p½r. В силу  имеем r=p. Это противоречит предположению, что r - составное число.

 

ЗАДАЧА 2. а) Найдите все простые числа p и q такие, чтобы  5p+7q и 7p+10q были простыми. б) Найдите все простые числа, не превышающие 400, при делении которых на 210 будет составной остаток.

 

Указание: а) при нечетных p и q четное число 5p+7q- составное, поэтому надо расматривать случаи, когда p=2 или когда q=2; б) при делении такого простого числа на 210 составными могут быть только остатки 11×11, 11×13 и 13×13 (обоснуйте!).

 

Тема 6. Элементы комбинаторики.

 

Ознакомимся  с начальными сведениями комбинаторики в процессе решения упражнения.

 

УРАЖНЕНИЕ 2.  Имеется 5 различных книг и 3 различных журнала, которые расставляют соответственно на книжную полку и на полку для журналов.

а) Сколькими способами  можно поставить на эти полки одновременно книгу и журнал?

б) Сколькими способами эти 5 книг можно поставить на книжную полку? Два способа расстановки считаем одинаковыми лишь в том случае, когда в результате расстановки каждым из них книги будут стоять на полке в одном и том же порядке.

в) Сколькими способами можно поставить 3 книги из 5 на книжную полку? Два способа расстановки считаем одинаковыми лишь в том случае, когда в результате расстановки каждым из них на полке будут одни и те же книги и в одном  и том же порядке.

г) Сколькими способами можно поставить 3 книги из 5 на книжную полку? Два способа  расстановки считаем одинаковыми лишь в том случае, когда в результате расстановки каждым из них на полке будут одни и те же книги.

д) Сколькими способами на эти полки можно поставить одновременно 3 книги и 2 журнала? Два способа расстановки считаем одинаковыми лишь в том случае, когда в результате расстановки каждым из них на полке будут одни и те же книги и журналы.

Решение.

а) Поставим какую-то книгу на полку, одновременно с ней мы можем поставить на журнальную полку один из трех журналов, т.е. существует три способа расстановки, в результате которых на книжной полке будет выбранная книга. Поскольку книг 5 и для каждой из них имеем три способа расстановки, то всего существует 5×3=15 способов.

ЗАМЕЧАНИЕ. Допустим имеем n множеств элементов, а в каждом из этих множеств по  элементов. Тогда число способов одновременного выбора по одному элементу из каждого из этих множеств равно  (обоснуйте!). Так, например, в нашей задаче было n=2,  и , поэтому число способов равнялось . 

б) Первую книгу можно выбрать пятью способами, вторую- четырьмя (так как одна уже выбрана), третью- тремя (так как две книги уже выбраны), четвертую- двумя и последнюю пятую- одним способом. Откуда находим 5×4×3×2×1=120- общее число способов расстановки книг на полке.

ЗАМЕЧАНИЕ. Если существует n элементов, то число способов расстановки их по порядку равно n×(n-1)×(n-2)×...×2×1. Каждую такую расстановку обычно называют перестановкой из n элементов, а число перестановок обозначают n! (читается: “n - факториал”). Для удобства считают 0!=1. Так, например, в нашей задаче было n=5 и поэтому число способов равнялось 5!=5×4×3×2×1=120.

в) Первую книгу можно поставить на полку пятью способами, вторую- четырьмя, а третью- тремя способами. Поэтому общее число способов равно 5×4×3=60.

ЗАМЕЧАНИЕ. Если имеется n элементов, то число упорядоченных наборов по k элементов () из этих   элементов равно n×(n-1)×...×(n-k+1) (обоснуйте!). Такие упорядоченные наборы называются размещениями из n элементов по k, а их число обозначают , т.е. . Так, например, в нашей задаче было n=5 и k=3 и поэтому число способов равнялось

г) Обратите внимание на схожесть вопросов в заданиях в) и г)! Число размещений (упорядоченных наборов) из 5 книг по 3 равно . Но каждой тройке книг (неупорядоченному набору) соответствует 3!=1×2×3=6 перестановок из этой тройки книг. Поэтому искомое число неупорядоченных наборов по три книги равно , т.е. имеем 10 способов.

ЗАМЕЧАНИЕ. Если имеется n элементов, то число неупорядоченных наборов по k элементов () равно  (обоснуйте!). Такие неупорядоченные наборы обычно называют сочетаниями из n элементов по k, а их число обозначают . Проверьте равенство: . Так, например, в нашей задаче было n=5 и k=3 и поэтому число способов равнялось .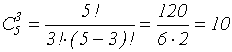

д) Сначала замечаем, что мы имеем дело с неупорядоченными тройками книг и парами журналов. Число способов выбора тройки  книг равно , а число способов выбора пары журналов равно . Поэтому общее число способов равно 10×3=30 (самостоятельно это обоснуйте по аналогии с заданием а).

 

ЗАДАЧА 3. В классе 25 учащихся, среди которых 12 девочек. а) Учитель должен вызвать к доске одновременно мальчика и девочку. Сколькими способами он может это сделать? б) Нужно выбрать старосту класса и его заместителя. Сколькими способами это можно сделать? в) Для участия в конкурсе художественной самодеятельности нужно выбрать два мальчика и три девочки. Сколькими способами это можно сделать?

 

ЗАДАЧА 4. Имеется набор из 30 двузначных натуральных чисел.

а) Для каждой тройки чисел из набора нашли их сумму. Докажите, что среди полученных сумм найдется по крайней мере 16 равных между собой.

б) Указанный набор разбили на два набора, в одном из которых 10 чисел, а в другом 20 чисел. Затем нашли сумму каждой пары чисел, взятых по одному из каждого полученного набора. Докажите, что среди полученных сумм найдется по крайней мере две равные между собой.

в) Имея два набора как и в пункте б), нашли сумму каждой четверки чисел, в которой два слагаемых из одного набора, а остальные два слагаемых из другого набора. Докажите, что среди полученных сумм найдется по крайней мере 24 равных между собой.

 

Указание: а) опредилите число таких сумм и заметьте, что суммы могут принимать значения только от 30 до 297, а далее по принципу Дирихле; б) указанные суммы принимают значения от 20 до 198; в) указанные суммы принимают значения от 40 до 396.

 

Тема 7. Инвариант.  

 

Инвариант - это то, что не меняется при определенных действиях. Умение находить инвариант часто помогает при решении некоторых задач.

УПРАЖНЕНИЕ 3. На доске написано число 876543210. За один ход разрешается стереть любые две цифры и вместо каждой из них написать большую или меньшую на 1 цифру. Можно ли за некоторое количество таких ходов получить на доске число 100000000?

Решение. Так как на доске за ход две цифры меняют свою четность на противоположную, то четность суммы цифр, записанных на доске, не меняется. Таким образом, в качестве инварианта можно рассматривать четность суммы цифр на доске. Так как у исходного числа суммы цифр 36 и является четной, то ни за какое число ходов мы не сможем получить число 100000000 с нечетной суммой цифр.

 

ЗАДАЧА 5. Вместо любых двух чисел а и b среди записанных на доске за один ход можно написать два числа 3×а+b и а+3×b. Можно ли из набора чисел 1,2,3,4 за несколько ходов получить набор 1,9,9,7; 1,9,9,8; 1,9,9,9; 2,0,0,0?

 

Указание: покажите, что остаток суммы чисел на доске при делении на 3 - инвариант.

 

Задача 6. По кругу по ходу часовой стрелки числами от 1 до 2000 пронумерованы 2000 фишек. За ход разрешается поменять местами любые две фишки, между которыми стоят ровно три фишки. Могут ли через несколько ходов фишки с номерами 7 и 1997 оказаться рядом?

 

 

Тема 8. Построение циркулем и линейкой.

 

Желательно ознакомиться с содержанием §5 в учебнике по геометрии 7 И.Ф. Шарыгина и §4.2 в учебнике по геометрии 7-11 А.В. Погорелова. Как правило, оформление задач на построения циркулем и линейкой дается в виде алгоритма, состоящего из простейших построений. К простейшим построениям относятся: 1) откладывание на луче отрезка, равного данному; 2) деление отрезка пополам или проведение серединного перпендикуляра к отрезку; 3) построение перпендикуляра из данной точки на данную прямую; 4) построение на луче в данной полуплоскости угла, равного данному; 5) построение биссектрисы угла; 6) построение прямой, параллельной к данной прямой и проходящей через точку вне ее. Иногда в ходе построений можно ссылаться на некоторые опорные построения: 1) построение треугольника по двум сторонам и углу между ними; 2) построение треугольника по стороне и прилежащим к ней углам; 3) построение треугольника по трем сторонам; 4) построение треугольника, равного данному; 5) описать около треугольника окружность; 6) вписать в треугольник окружность; 7) провести касательную из внешней точки к окружности и пр..

Сначала полезно решить две очень важные задачи (можно использовать учебник).

 

ЗАДАЧА 7. Докажите, что около треугольника можно описать и притом одну окружность.

 

ЗАДАЧА 8. Докажите, что в треугольник можно вписать и притом одну окружность.

 

Полезно знать два способа построения касательной из внешней точки к окружности (§4.2 в учебнике И.Ф. Шарыгина и §11 в учебнике А.В. Погорелова). Это поможет в решении некоторых из предлагаемых ниже задач, в которых имеются ввиду построения только с помощью циркуля и линейки.

 

ЗАДАЧА 9. Постройте треугольник по двум сторонам и высоте к первой из этих сторон.

 

Указание: отметим, что по этим данным можно построить два разных треугольника.

Особую роль играет метод геометрических мест точек (см. §41 и §5 в указанных ранее учебниках)

 

ЗАДАЧА 10. В плоскости дан разносторонний треугольник АВС. Постойте ГМТ (геометрическое место точек), равноудаленных от точек В и С, а также от прямых АВ и АС.

 

ЗАДАЧА 11. На плоскости даны точки А, В, С и D. Постройте ГМТ, состоящее из точек М, из которых отрезок АВ виден под углом в 90°, причем СМ=DМ. Всегда ли есть решение?

 

ЗАДАЧА 12. На данной прямой постройте все точки, из которых отрезки касательных к данной окружности равны данному отрезку.

 

Попробуйте решить следующие две задачи (первую из них приписывают Герону!).

 

ЗАДАЧА 13. В одной полуплоскости относительно прямой j даны две точки А и В. Опредилите на прямой j точку М такую, чтобы АМ + МВ было наименьшим. Постройте ее.

 

Указание: если А симметрична к А относительно j, то М -пересечение прямых АВ и  j.

 

ЗАДАЧА 14. Внутри угла АОВ дана точка С. Постройте на прямых ОА и ОВ такие точки М и N, чтобы периметр треугольника СМN принимал наименьшее возможное значение.