Тема 1. Игры.

 

В этой части заочной школы вы познакомитесь с задачами - играми. Во всех играх предполагается, что играют двое, ходы делаются по очереди (игроки не могут пропустить ход). Ответить всегда надо на один и тот же вопрос – кто побеждает: начинающий (первый) или его партнер (второй) ?

Способ игры, обеспечивающий выигрыш одному из партнеров в любом случае, как бы ни играл  его противник, называется “выигрышной стратегией”. Это тот секрет , обладая которым вы сможете выиграть у самого сильного противника. Наша цель – научится находить “ключ к победе” в различных играх, грамотно формулировать стратегию и доказывать, что она действительно ведет к выигрышу.

Один из путей поиска выигрышной стратегии – анализ игры с ее конца.

Упражнение 1. Напишите в тетради в ряд числа от 0 до 14 в порядке  возрастания. обведите каждое число в кружок. Один из кружков закройте фишкой. За ход разрешается передвинуть фишку влево на один, два, три, или четыре кружка. Проигрывает тот, кому некуда ходить. При каком начальном положении фишки выигрывает начинающий ?

Решение. Найдем выигрышные начальные позиции фишки, при которых начинающий выигрывает  (отметим соответствующие кружки знаком “+” , проигрышные “–” ). Начнем с конца. Завершающая позиция игры – фишка на кружке 0 –проигрышная (начинающему некуда ходить), ставим “–”. Кружки 1, 2, 3, 4 отмечаем плюсами, т.е. если фишка на этих кружках, начинающий выигрывает  за 1 ход , ставя фишку на 0. Если фишка на кружке 5, то за ход начинающий окажется в кружках 1, 2, 3 или 4. Партнер пойдет в 0 и выиграет. Значит, кружок 5 – проигрышный (ставим ” –”). Кружки 6, 7, 8, 9 выигрышные,  т.к. начинающий передвигает фишку в 5 и выигрывает. Аналогично получаем , что кружки 10, 15 и т.д. проигрышные. Вывод: начинающий выиграет, если каждый раз будет ставить фишку на клетку с номером, кратным 5, причем начальное положение фишки на номере, не кратном 5. В противном случае этой стратегией может воспользоваться противник.

 

Задача 1.  Из кучи камней двое играющих по очереди берут 1, 2, 3 или 4 камня. Выигрывает тот,  кто возьмет последний камень. При каком начальном количестве камней выигрывает начинающий ?

Задача 2. Игра начинается с числа 0. За ход разрешается прибавить к имеющемуся числу любое натуральное число от 1 до 9. Выигрывает тот, кто получит число 100. Какой игрок выиграет и при какой стратегии ?

 

Существует так называемые игры - шутки, исход которых не зависит от того, как играют соперники. Для решения такой игры не нужно указывать выигрышную стратегию. Достаточно лишь доказать, что выигрывает тот или иной игрок ( независимо от того, как они будут играть). Приведем пример такой игры.

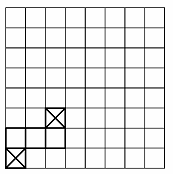
Упражнение 2. Каждый из двух игроков по очереди разрезает данную фигуру. За один ход разрешается любую из имеющихся частей разрезать прямолинейно по границе двух цветов на новые две части. Проигрывает тот, кто не может сделать разрез. Какой игрок выигрывает ?

Решение. Сначала была одна целая часть. В конце игры, когда нельзя сделать ни одного хода, фигура разрезана на 25 кусочков. Таким образом, всего можно сделать 24 разреза. Последний, 24‑й разрез (так же, как и все другие разрезы с четными номерами) делает второй игрок. Значит, выигрывает тот, кто “ходит” вторым, независимо от того, как он будет играть.

 

Задача 3. Имеются 3 букета цветов: в первом – 10, во втором – 15, в третьем – 20 цветков. За ход разрешается разбить любой букет на 2 меньших; проигрывает тот, кто не может сделать ход. Какой игрок выиграет и почему ?

 

Рассмотрим теперь задачи на так называемую “симметричную стратегию”.

Упражнение 3. Имеется 2 коробки конфет – по 20 в каждой. За  ход разрешается взять любое количество конфет, но только из одной коробки. Проигрывает тот, кому нечего брать.

Решение. Второй игрок побеждает при помощи симметричной стратегии: за каждый свой ход он должен брать столько же конфет, сколько за предыдущий ход взял первый игрок, но из другой коробки. Таким образом, у второго игрока всегда есть ход. Симметрия здесь состоит в равенстве числа конфет в коробках.

 

Задача 4. Есть числа 20 и 30. За ход разрешается вычитать из одного из них любое натуральное число, не большее исходного. Выиграет тот, кто первым получит два нуля. Какой из игроков выиграет и как он должен играть?

 

Симметричная стратегия чаще всего имеет чисто геометрический смысл.

Упражнение 4. Двое по очереди кладут  пятаки на круглый стол, причем так, чтобы они не накладывались друг на друга.  Проиграл тот, кто не может сделать ход.

Решение. Выигрывает 1‑й, независимо от размеров стола. Первым ходом он кладет монету так, чтобы центры стола и пятака совпадали. После этого на каждый ход 2‑го игрока первый отвечает симметрично относительно центра стола. После каждого хода 1‑го игрока позиция симметрична. Поэтому, если возможен очередной ход  2‑го игрока, то возможен и симметричный ответный ход 1‑го. Значит, он побеждает.

 

Задача 5. Двое по очереди ставят королей в клетки доски  так, чтобы короли не били друг друга. Проигрывает тот, кто не может сделать ход. Какой из игроков выиграет и как он должен играть ?

 

Тема 2.  Инвариант.

 

Пусть имеются некоторые объекты, над которыми можно выполнять определенные операции. Спрашивается – можно ли из одного объекта получить другой с помощью этих операций ? Чтобы дать правильный ответ, необходимо найти в задаче такую величину, которая не меняется при указанных операциях. Такая величина называется инвариантом.

Упражнение 5. С набором из 7 чисел, каждое из которых равно 1 или -1 разрешается проделывать операцию: поменять знак одновременно у каких-нибудь 2-х чисел. Можно ли с помощью нескольких таких операций получить из набора

 1  -1  -1   1   1   1   1  набор 1   1   1   1   1 -1   1?

Решение. Нет, т.к. при нашей операции число минусов всегда будет оставаться четным (это инвариант), а во втором наборе минусов нечетное число (один).

 

Задача 6. Имеется 16 спичечных коробков, один из которых закрыт. За один шаг разрешается либо закрыть, либо открыть любые 2 из них. Можно ли, повторяя эти операции, добиться, чтобы все коробки оказались закрытыми ?

 

Задача 7. На столе лежат 15 шашек. Семь из них – донышком вверх, а остальные восемь – “дамки”. За один ход разрешается переворачивать любые 2 шашки. Можно ли сделать так, чтобы все шашки стали “дамками” ?

 

Задача 8. В ряд разложены фишки от 1 до 56. За каждый ход разрешается поменять местами любые 2 фишки, между которыми стоит ровно одна фишка. Можно ли через несколько ходов фишки с номерами 5 и 56 поменять местами ?

 

Инвариантом может быть не только четность. Попробуйте самостоятельно решить задачу, в которой в качестве инварианта выступает цвет шахматного поля.

 

Задача 9. Юра придумал новую шахматную фигуру, которая “ходит” так, как показано на рисунке. Сможет ли он за несколько ходов переставить эту фигуру с какого-то исходного поля на соседнее ?

 

Тема 3.  Графы.

 

Не отрывая руки от бумаги и не проводя по линии дважды, начертите фигуру, изображенную на рисунке. Вам не удалось решить эту задачу ? Сейчас объясним почему.

Назовем наш рисунок графом. Такое название можно дать любому набору точек (вершин), некоторые из которых соединены между собой линиями (ребрами). Количество ребер, выходящих из одной вершины, назовем степенью этой вершины. На нашем графе 9 ребер; 3 вершины степени 5 и одна степени 3 (см. рисунок), т.е. 4 нечетных вершины.

Следующее утверждение дает ответ на вопрос, почему не удалось решить указанную задачу: если на фигуре (на графе) больше двух нечетных вершин, то ее нельзя нарисовать одним росчерком.

 

а)                   б)                  в)                   г)                       д)

Задача 10. Укажите, какие из приведенных знаков и символов нельзя нарисовать одним росчерком и объясните,  почему:

 

Упражнение 6. Одному архитектору было поручено спроектировать подземный лабиринт из 9 комнат с  условием, что каждая комната должна соединятся коридорами ровно с тремя другими. Возможен ли такой проект ?

Решение. Предположим возможен. Рассмотрим граф: коридоры – ребра графа; комнаты – вершины (их по условию 9 и степень каждой равна трем). Чтобы подсчитать количество ребер графа, просуммируем степени его вершин. При таком подсчете каждое ребро учитывается дважды (т.к. соединяет 2 вершины). Значит число ребер 9×3/2.  Т.к. это число не целое, то такого графа не существует. Мы получили формулу:

 

Число ребер графа = (Сумма степеней вершин) / 2

 

Из нее следует. что сумма степеней всех вершин графа должна быть четной, иначе число ребер будет дробным.

 

Задача 11. Докажите, что число нечетных вершин любого графа – четно.

 

Задача 12. Предприятие закупило 17 компьютеров. Можно ли их соединить сетью так, чтобы было 8 компьютеров, каждый из которых связан с пятью другими; 5 компьютеров, каждый из которых – с тремя другими и 4 – с двумя другими ?

 

 

Тема 4.  Принцип Дирихле.

 

Рассмотрим принцип Дирихле на примере:

Упражнение 7. Пусть есть 10 клеток, в которых надо разместить 11 зайцев. Докажите, что по крайней мере в одной клетке будет 2 зайца.

Решение. Разделим 11 на 10 с остатком: 11=10×1+1. В худшем случае посадим в каждую клетку по одному зайцу (частное). Таким образом рассадим 10 зайцев (делитель), один окажется лишним (остаток). Он и будет вторым в какой-то клетке.

Для запоминания удобна следующая формулировка принципа Дирихле: если в N клетках сидит не менее N + 1 зайцев, то в какой-то из клеток сидит не менее двух зайцев.

 

Задача 13. На 12-ти книжных полках требуется разместить 315 книг. Докажите, что по крайней мере на одной книжной полке будет стоять не менее 27 книг.

 

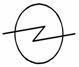Задача 14. Шесть гроссмейстеров одержали победу в 20 шахматных партиях, каждый выиграл хотя бы одну встречу. Докажите, что хотя бы два из них одержали одинаковое число побед.