Тема 1.  Дробные числа и действия над ними.

 

В предыдущих темах мы имели дело с натуральными и целыми числами, рассмотрим теперь некоторые вопросы, связанные с дробными числами. В средние века (500–700 лет тому назад) учение о дробях считалось самым трудным разделом арифметики, но сейчас с этими числами успешно действуют ученики, начиная с 5 класса. Дроби появляются при делении целых чисел и при измерении величин.

Древние египтяне 3500 лет тому назад уже имели представление о дробных числах и действиях над ними, но, кроме дроби  типа , они использовали исключительно дроби с постоянным числителем – единицей, например,  и т.д.; дробь  они выражали в виде суммы , а дробь  в виде суммы  (Проверьте верность этих представлений).

 

Задача 1.  В виде суммы каких дробей с числителями единица древние египтяне представляли:    а)    б) ?

 

Прием древних египтян используется при решении следующего упражнения:

Упражнение 1. Пусть у четырех учеников имеется три арбуза, каким образом разделить эти арбузы между ними так, чтобы каждому досталось поровну и ломти делимых арбузов были по возможности более крупными?

Решение. Так как , то достаточно дать каждому ученику по половине арбуза и четверти арбуза, а для этого достаточно два арбуза разделить пополам, а третий арбуз на четыре равные доли.

 

Задача 2. Как разделить поровну и наиболее рациональным способом семь арбузов между восемью учениками?

 

Знаменитый древнегреческий философ и математик Пифагор (около 2580 – 2500 лет тому назад) на вопрос правителя острова Самос Поликрата, сколько у него учеников, ответил: “Половина моих учеников изучает прекрасную математику, четверть исследует тайны вечной природы, седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь к ним еще трех юношей, из которых Теон превосходит прочих своих способностями. Сколько учеников я веду к рождению истины?” Попробуйте определить на основе рассказа Пифагора сколько было у него учеников. Это можно сделать с помощью действий над дробями!

Две дроби  и  считаются равными, если равны произведения ad = bc. Например, как легко проверить, равны следующие дроби: , из этих дробей простейшая , это несократимая дробь, т.е. числитель и знаменатель ее не имеют общих натуральных делителей, отличных от 1, остальные дроби сократимы, что видно из равенств: ;   ;   ; .

Среди всех дробей, равных дроби , есть единственная равная ей несократимая дробь  и, чтобы ее найти надо числа a и b (числитель и знаменатель дроби) разделить на их наибольший общий делитель d, тогда 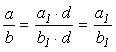 и последняя дробь  будет несократимой. Сокращение дробей не всегда простая задача.

 

Задача 3. Сократить до несократимых дробей следующие дроби:   а) ;    б) ;   в)  .

Задача 4. Какое число надо вычесть из числителя дроби  и прибавить к знаменателю, чтобы после сокращения получить ?

 

Задача 5. Если к числителю некоторой дроби прибавить 4, а к знаменателю 10, и сократить получившуюся дробь, то получится исходная (первоначальная) дробь. Указание: пусть исходная дробь , тогда по условию .

 

Упражнение 2. При каких натуральных n дробь  будет равна натуральному числу?

Решение. Так как 32 имеет делители 1, 2, 4, 8, 16, 32,  то  n+1 должно быть равно одному из этих делителей. Если  n+1=1, то n=0,  но это значение n не подходит, т.к. 0  не натуральное число. Если  n+1=2, то  n=1; если n+1=4, то n=3; если n+1=8, то n=7; если n+1=16, то n=15; если n+1=32, то n=31.  Итак, получим следующие возможные значения для  n=1, 3, 7, 15, 31.

 

Задача 6. При каких натуральных n дробь  будет рана натуральному числу?

 

Дробь , где a и b – некоторые натуральные числа, называется правильной, если ее числитель меньше знаменателя, т.е.  a < b; если же числитель дроби больше ее знаменателя, т.е.  a > b, то дробь  называется неправильной. По теореме о делении с остатком (в случае  a > b) существует такое натуральное число q и целое r, что выполняется равенство a=b×q+r, где  0£r<b.  Деля каждое слагаемое равенства a=b×q+r на b получим такое равенство дробей: , откуда . Таким образом, неправильная дробь  представлена в виде суммы натурального числа q и правильной дроби , в этом случае число q называют целой частью дроби , а правильную дробь  ее дробной частью.

 

Задача 7. Представьте следующие неправильные дроби в виде суммы натурального числа и правильной дроби, а также выясните между какими натуральными числами заключены эти неправильные дроби: а); б); в).

 

Дробь  меньше дроби , если произведение a×d меньше произведения b×c. Отсюда следует, что дробь  меньше дроби , если a меньше m. Пусть n – натуральное число. Ряд расположенных в порядке возрастания несократимых правильных дробей с натуральными знаменателями, не превосходящими n, называется в теории чисел рядом Фарея, отвечающим числу n. Например, при n=2 ряд Фарея состоит из одной дроби ; при n = 3 ряд Фарея есть , , . Ряд Фарея, отвечающий данному натуральному числу n, может быть построен следующим образом: пишем дроби ,  , если 2 £  n, то между этими дробями помещаем еще дробь , затем в полученном ряде дробей , ,  между каждыми двумя соседними дробями  и  с b₁ + d₁ £n помещаем дробь 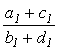 и этот процесс продолжаем до тех пор, пока это возможно. Например, если надо построить ряд Фарея, отвечающий n=3, то в ряде полученном ранее  , ,  помещаем между  и  дробь =, а между  и  помещаем дробь , получаем ряд , процесс закончен (т.к. n=3), исключая из полученного ряда крайние дроби (они служили нам для построения ряда)  и  получаем искомый ряд дробей Фарея, отвечающий  n=3.

Если n = 4, то в полученном ранее ряде дробей  между  и  помещаем дробь ; между  и  ничего не помещаем, т.к.  3+2=5>4, аналогично по той же причине ничего не помещаем между дробями  и , а между  и  помещаем дробь , получим ряд возрастающих по величине дробей , исключаем крайние дроби и получаем ряд Фарея для n=4: .

 

Задача 8. Построить ряд Фарея, отвечающий числу n, если:  а)  n=5;   б)  n=6.

 

Дроби  и  складываются, вычитаются, умножаются и делятся по известным правилам: ; ; ; 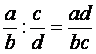. При сложении и умножении дробей выполняются переместительные и сочетательные законы, как и для сложения и умножения целых чисел, что позволяет иногда упрощать вычисления.

Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых. Например, среднее арифметическое двух чисел a и b есть дробь , а среднее арифметическое трех чисел a, b, c есть дробь .

Упражнение 3. Саша, Вова, Коля и Петя собирали грибы. Саша нашел 8 грибов, Вова 12 грибов, Коля 9, а Петя 7. Мальчики решили поделить грибы поровну, как это сделать?

Решение. Так как мальчиков четыре, то среднее арифметическое четырех чисел 8, 12, 9, 7 будет  и значит каждому из ребят досталось по 9 грибов.

 

Задача 9. Если бы Саша нашел 11 грибов, Вова 10, Коля 9, а Петя 7 грибов и ребята по прежнему хотели бы распределить грибы поровну, то как они должны были бы поступить ?

 

Если мы путь в S километров проходим (или проезжаем) за t часов, то дробь  выражает нашу среднюю скорость, т.е.  километров мы проходили в среднем за каждый час.

Упражнение 4. Автобус ехал по дороге в гору от пункта А в пункт В со скоростью 40 км/ч, а обратно из пункта В в пункт А под гору он ехал со скоростью 60 км/ч. Какова средняя скорость автобуса на трассе?

Решение. Пусть S – расстояние между пунктами А и В, тогда из А в В автобус ехал  часов, а обратно он ехал  часов. Всего на поездку из А в В и обратно автобус затратил  часов. Следовательно его средняя скорость равна 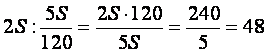км/ч.

Аналогичным способом решается следующая задача:

 

Задача 10. Автобус проехал три равных по длине участка пути: первый со скоростью 50 км/ч,  второй 30 км/ч, а третий 60 км/ч.  Какова средняя скорость движения автобуса на всем пути?

 

Упражнение 5. Расстояние между пунктами А и В равно 20 км. Из пункта А в пункт В вышел турист с постоянной скоростью 4 км/ч, а из пункта В в пункт А одновременно с ним выехал велосипедист. С какой постоянной скоростью надо ехать велосипедисту, чтобы он встретился с туристом через  часа.

Решение. Пусть x км/ч - постоянная скорость велосипедиста, тогда турист и велосипедист сближаются со скоростью (x+4)км/ч, следовательно из условия должно выполняться равенство , следовательно  3×20=2×(4+x), откуда 60=8+2x и значит 52=2x, а потому x=26 км/ч.

А теперь попробуйте решить задачу на движение И.Ньютона (1641 – 1727).

 

Задача 11. Два почтальона А и В находятся друг от друга на расстоянии 59 миль (одна миля равна 1, 609 км). Утром они отправились друг другу навстречу. А проходит в два часа 7 миль, В проходит в три часа 8 миль, но В выходит часом позже, чем А. Сколько миль пройдет А до встречи с В?

 

С помощью дробей решаются задачи на наполнение бассейнов, которые составлялись и 100 и 200 и 300 и 1000 и 2000 лет тому назад!

 

Задача 12. Один  кран наполняет бак водой за 4 часа, второй кран наполняет его за 3 часа, а третий кран наполняет бак за 5 часов.

а) Какая часть бака наполняется первым краном за 1 час?

б) За какое время первый и второй краны наполнят бак, работая  одновременно?