8 класс - Заочная математическая школа

*Заочная математическая школа

8-й класс (1-я часть)

Составитель доценты КубГУ Титов Г.Н. и Сергеев Э.А.

5 класс

6 класс

7 класс

8 класс

Задача 1.

Упростите выражение и выясните при каких значениях a и b оно определено:

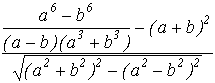
Задача 2.

Решите уравнение:

§1. Десятичная запись. Делимость целых чисел.

Всякое натуральное число n в десятичной записи имеет вид , где - цифры, причем . Сформулируйте и докажите признаки делимости натуральных

чисел на числа 2, 5, 4, 25, 3, 9, 8, 16, 11, а также на числа 6, 10, 12, 15, 18, 20 и 36.

Например, сформулируем и докажем признак делимости на 9.

Пример 1. Доказать, что натуральное число n делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

Решение. Имеем:

и,

так как числа ,...,10-1=9 делятся на 9, то из предыдущего равенства следует,

что n делится на 9 в том и только в том случае, когда сумма его цифр делится на 9.

Задача 3.

Натуральное число записано в десятичной системе при помощи единиц, двоек и пятерок.

Причем единиц в два раза больше, чем двоек, а пятерок столько же сколько двоек.

Докажите, что число n составное.

Пусть a и b - целые числа, где , тогда существуют однозначно определенные целые числа q и r такие,

что и а=bq+r. Это теорема о делении с остатком, при этом число а- делимое, b- делитель, q- частное

и r- остаток.

Пример 2. Написать общий вид целых чисел, которые при делении на 12 дают остаток 5.

Очевидно, это числа вида 12×k+5, где k пробегает множество всех целых чисел.

Задача 4.

Найдите наименьшее натуральное число, которое при делении на 2, 3, 4, 5, 6, 7 и 8 дает остаток 1.

Какой общий вид этих чисел?

Любое четное число имеет вид 2×k, а нечетное 2×k+1, где k- некоторое целое число;

любое целое число имеет также вид 3×k+r, где r=0, или r=1, или r=2.

Пример 3.

Найти значения остатков при делении квадратов целых чисел: а) на 4; б) на 3.

Решение. Так как (2×k)²=4×k² и (2×k+1)²=4×k²+4×k+1=4×(k²+k)+1,

то при делении на 4 могут лишь быть остатки 0 или 1.

Аналогично проверяется, что квадраты целых чисел при делении на 3 дают остатки 0 или 1.

Задача 5.

Доказать что уравнение :

а) при n=1 и n=4 имеет более одного решения в целых числах;

б) при n=2, n=3 и n=8 не имеет решений в целых числах.

Каждое натуральное число n>1 однозначно (с точностью до порядка следования сомножителей)

представляется (факторизуется) в виде произведения простых чисел.

Пример 4. Сколько существует натуральных чисел, меньших 1997 и не делящихся на 11?

Решение. Найдем сначала число чисел не превосходящих 1997 и делящихся на 11.

Их общий вид: 11×k, где k-натуральное число и . Так как 1997=11×181+6,

то получаем и чисел, меньших 1997 и делящихся на 11 будет 181.

Следовательно, натуральных чисел, не делящихся на 11 и не превосходящих 1997,

будет .

Задача 6.

Сколько существует натуральных чисел, меньших 1997 и не делящихся ни на 11, ни на 17?

Пример 5. Доказать, что существует бесконечно много целых значений n, для которых число делится на 13.

Решение. Имеем тождество

, из которого следует,

что делится на 13 только если (n+7) делится на 13, т.е. должно быть n+7=13×k и,

значит, n=13×k–7, где k пробегает множество целых чисел. Все доказано.

Задача 7.

Доказать, что ни при каком целом n число не делится на 169.

Пример 6. Доказать, что всякое нечетное число можно представить в виде разности квадратов

двух целых чисел.

Решение. Пусть 2×k+1=a²–b²=(a–b)×(a+b), тогда можно взять a–b=1 и a+b=2×k+1.

Откуда при всех целых k числа a=k+1 и b=k тоже будут целыми.

Задача 8.

Можно ли представить в виде разности квадратов двух целых чисел числа:

а) 1996; б) 1998 ?

Какие четные натуральные числа можно представить в виде разности квадратов двух целых чисел?

Задача 9.

Доказать, что число 19 можно единственным образом представить в виде разности кубов

двух натуральных чисел. Всякое ли простое число можно представить в виде разности кубов

двух натуральных чисел?

Известно, что если p является наименьшим простым числом, делящим составное число n,

то . В частности, если натуральное число m>1 не делится на простые числа, не

превосходящие m, то m является простым числом. Попробуйте это доказать.

Задача 10.

Разложить в произведение простых множителей числа:

а) 9991;

б) 1000001.

Задача 11.

Доказать, что если p и - простые числа, то тоже простое.

§2. Углы, связанные с многоугольником и окружностью.

Известно, что сумма всех внутренних углов любого n-угольника равна (n-2)×180°.

Оказывается, что сумма всех внешних углов выпуклого многоугольника равна 360°.

Докажите последнее утверждение самостоятельно.

Задача 12.

а) При каких n все углы правильного n-угольника измеряются целыми числами градусов?

б) Существует ли выпуклый 1997-угольник, у которого все углы измеряются целыми числами градусов?

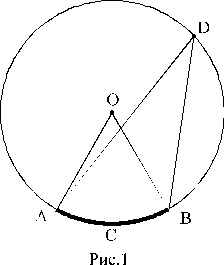
Особое место в геометрии занимает тема нахождения углов, связанных с окружностью.

На рисунке 1 изображен центральный угол ÐАОВ, опирающийся на дугу ÈАСВ,

а также вписанный угол ÐADB, опирающийся на эту же дугу.

Под угловой величиной дуги понимают угловую величину, опирающегося на нее центрального угла

и пишут ÈACB = ÐAOB.

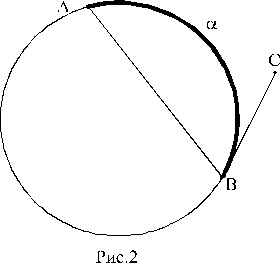
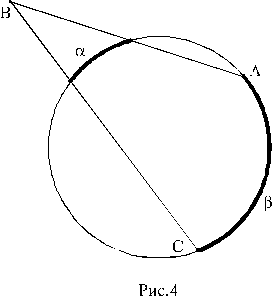
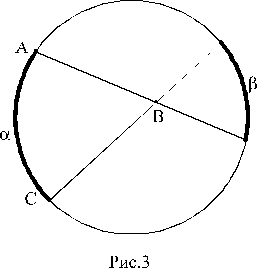
На рисунках 2, 3 и 4 буквы a и b указывают угловые величины отмеченных дуг.

Имеют место следующие равенства:

1. ÐADB = ÈACB (рис. 1);

2. ÐABC =α/2, где ВС- касательная к окружности (рис.2);

3. ÐABC = (a+b)/2 (рис.3);

4. ÐABC = (b–a)/2 (рис.4).

Ознакомьтесь с доказательством равенства 1 (см., например, учебник А.В.Погорелова, §107).

Задача 12.

Докажите равенства 2-4.

Задача 13.

Докажите, что около четырехугольника можно описать окружность тогда и только тогда, когда сумма его каких-то двух противоположных углов равна 180°.

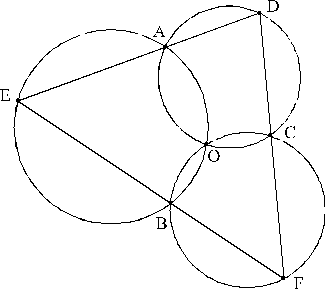
Задача 14.

Три окружности пересекаются в одной и той же точке О. Кроме этого первая окружность пересекает вторую еще в точке А, вторая третью–в точке В, а третья первую–в точке С (см. рис.). Точка D лежит на первой окружности, а прямые DA и DC пересекают вторую и третью окружности соответственно в точках E и F. Докажите, что точки F, B и E лежат на одной прямой.