Тема 1. Десятичная запись натурального числа.

 

Первые представления о числе приобретены людьми с незапамятной древности. Они возникли изсчета людей, животных, плодов, различных изделий человека и других предметов. Результатом счета являются числа 1, 2, 3, 4, 5,… Этот ряд продолжается без конца; он называется натуральным рядом, а числа–натуральными.

Способы записи чисел называют системами счисления. Нашу систему счисления называют позиционной, т.к. каждая из цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) имеет различное значение в зависимости от позиции цифры в записи числа. Например, каждая цифра 3 в записи числа 333 имеет различное числовое значение: первая слева обозначает 3 сотни, вторая – 3 десятка, третья – 3 единицы. За основание нашей системы счисления взято число 10, поэтому она называется десятичной.

Любое натуральное число в десятичной системе счисления можно записать в виде суммы числа единиц, десятков, сотен и т.д. Например, запись 27 354 выражает, что в составе числа имеются 4 единицы, 5 десятков, 3 сотни, 7 тысяч и 2 десятка тысяч. В виде суммы оно запишется так:

27 354=2 · 10 000 + 7 · 1 000 + 3 · 100 + 5 · 10 + 4.

В общем случае, если в составе числа c единиц, b десятков, a сотен и т.д. , то пользуются записью:

.

 

Задача 1.

Двузначное число разделили на его первую цифру. В результате получили 14. Найти все такие двузначные числа.

 

Задача 2.

У трехзначного числа поменяли местами последние 2 цифры. В результате число уменьшилось на 18. Найдите это число.

 

 

Тема 2. Деление с остатком.

 

Известно, что всякое натуральное число a можно разделить на другое натуральное число b с остатком, т.е. единственным образом представить a в виде:

a=b×q+r,      0£r<b (*)

В этом случае число a называется делимым, b – делителем, q – неполным частным, r – остатком от деления a на b. Если r=0, то говорят, что a делится нацело на b и обозначают a½d.

 

Упражнение 1. Пусть b=14. Представьте в виде (*) числа: a=177; 154; 12.

Решение:

177=14·12+9,    0 < 9 < 14

154=14·11+0,    0 = 0 < 14

12=14·0+12,     0 < 12 < 14 .

 

Задача 3.

Число a разделили на b, получили неполное частное q и остаток r. Могут ли все числа a, b, q и r быть нечетными ? Ответ поясните.

 

Задача 4.

В страну Арифметику прибыла “делегация” чисел, при делении которых на 11 получались частные равные остаткам. Какой вид имели эти числа и сколько их было?

 

 

Тема 3.  Правила нахождения остатков.

 

 Рассмотрим правила нахождения остатков при делении натуральных чисел на 2, 3, 4, 5, 10, 25:

1. Число делится на 2 (на 5, на 10), если его последняя цифра делится на 2 (на 5, на 10);

2. Число делится на 4  (на 25), если число, записанное двумя его последними цифрами, делится на 4 (на 25);

3. Число делится на 3 (на 9), если сумма его цифр делится на 3 (на 9).

 

Упражнение 2. Получить указанные правила на примере делимости трехзначных чисел.

Решение. Воспользуемся свойством: если  и , то

1. . Пусть левая часть равенства делится на 2, тогда так как в правой части первое слагаемое делится на 2 (в разложении его на множители есть число 2), то число c тоже должно делиться на 2. Получили. что последняя цифра c числа  делится на 2. Аналогично доказывается для делимости на 5 и 10 (доказательство провести самостоятельно).

2. . Пусть  делится на 4. Так как в правой части 100×а делится на 4, то  тоже должно делится на 4, т.е., число, записанное двумя последними цифрами делится на 4.

3.. Пусть . Так как в правой части  то a+b+c тоже должно делится на 3. Получили что сумма цифр числа  делится на 3. Докажите самостоятельно для делимости на 9.

Сформулируйте признаки делимости чисел на 2, 3, 4, 5, 10, 25.

 

Упражнение 3. Докажите, что если в трехзначном числе средняя цифра равна сумме крайних, то число делится на 11.

Решение. Если цифры числа (слева направо) a, a+b, b, то само число: .

Получили, что в разложении числа на множители есть 11, следовательно, число делится на 11.

 

Задача 5.

Из трех различных цифр, отличных от нуля составили всевозможные двузначные числа так, что цифры в записи числа не повторялись. Докажите, что сумма всех полученных чисел делится на 22 независимо от исходного  выбора цифр.

 

Задача 6.

Докажите, что число  составное.

Если натуральные числа a и b делятся на некоторое натуральное число d, то d называется их общим делителем. Наибольший из общих делителей называется их наибольшим общим делителем и обозначается НОД(a, b). Если НОД(a, b)=1, то числа a и b называют взаимно простыми.

Упражнение 4. Найти все пятизначные числа вида 34x5y, каждое из которых делится на 36.

Решение. Число 36 можно представить в виде произведения взаимно простых чисел 9 и 4, следовательно, искомые числа делятся на 4 и 9. Число 5y должно делиться на 4, значит y=2 или y=6. 3+4+x+5+y=12+x+y должно делится на 9. При y=2 находим такую цифру x, чтобы , отсюда x=4. При y=6 , отсюда x=0 или x=9. Значит, условию задачи удовлетворяют три числа: 34 452, 34 056, 34 956.

 

Задача 7.

Какую цифру поставить вместо * в шестизначном числе 123 45*, чтобы оно делилось на 6 ?

 

Задача 8.

Чтобы получить доступ к  секретной информации компьютера, необходимо набрать код – четырехзначное число. Известно, что 1-я и 3-я цифра кода – единицы, а все число делится на 15, но не делится на 2. Найдите минимальное количество кодов, которые нужно перебрать, чтобы обнаружить искомый код.

 

 

Тема 4. Алгоритм Евклида.

 

 Повторите метод нахождения НОД натуральных чисел (через разложение на простые множители) .

Для разыскания НОД чисел применяется и другой метод. Он называется алгоритмом Евклида. Познакомимся с алгоритмом Евклида на примерах.

 

Упражнение 5. Найти:

а) НОД(6621,111); б) НОД(40,5).

 

Решение.

а) Делим 6621 на 111 с остатком:

6621=111·59+72, 0<72<111

Теперь делим делитель 111 на остаток 72:

111=72·1+39, 0<39<72

Снова делим делитель на остаток  и  т.д.

72=39·1+33,    0<33<39

39=33·1+6,      0<6<33

33=6·5+3,        0<3<6

6=3·2+0.

Процесс закончен, если на некотором шаге получаем остаток, равный нулю. НОД данных чисел равен последнему отличному от нуля остатку в алгоритме Евклида. В нашем случае это 3, т.е. НОД(6621,111)=3. Процесс, описанный в алгоритме Евклида не бесконечен, так как остатки убывают, оставаясь неотрицательными, а самый маленький из них ноль: 72>39>33>6>3>0=0.

б) Разделим 40 на 5: 40=5·8+0. На первом шаге получили остаток 0. В этом случае НОД(40,5) равен меньшему из чисел, т.е. 5.

Если натуральное число k делится на числа a и b, то оно называется общим кратным чисел a и b. Наименьшее из таких общих кратных называется наименьшим общим кратным чисел a и b и обозначается НОК(a, b).

Повторите метод нахождения НОК чисел (через разложение на простые множители) .

НОК двух чисел равно их произведению, деленному на их НОД, т.е.

 

Задача 9.

Пользуясь алгоритмом Евклида, найдите НОД и НОК номера вашего дома и почтового индекса.

 

Задача 10.

Из победителей математической олимпиады был сформирован отряд, в котором больше 100, но меньше 150 детей. Для отправки в летнюю математическую школу их разместили вначале в 8, а затем в 10 автобусах. При этом в обоих случаях детей в автобусах оказалось поровну. Сколько в отряде было девочек и мальчиков, если девочек было на 40 человек меньше, чем мальчиков?

 

Чтобы найти НОД трех чисел a, b, c , находим НОД(a,b)= d; затем НОД(d,c)= f, тогда НОД(a,b,c)=f.

 

Задача 11.

Для учеников трех шестых классов школа к новогоднему вечеру закупила шоколадные конфеты: 390, 405 и 420 штук. Сколько подарков получил каждый класс, если в каждом подарке одинаковое количество конфет и число их – наибольшее из всех возможных.

 

Задача 12.

Решить уравнения:

а)    б)    в) ;       г)  

 

Задача 13.

Даны две равные дроби. Одна из них , а сложив числитель со знаменателем второй дроби, получили 91. Найдите вторую дробь.

 

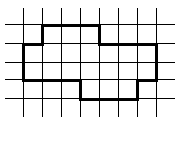
Задача 14.

Укажите различные способы разрезания данной фигуры на 4 равные части, чтобы линия разреза шла по сторонам клеток. (Способы считаются различными, если части, получаемые при одном способе разрезания не равны частям, полученным при другом способе).