*Заочная математическая школа
7-й класс (1-я часть)
Составитель доцент КубГУ Титов Г.Н.
5 класс
6 класс
7 класс
8 класс
Повторите материал из главы учебника по алгебре для 7 класса под редакцией С.А.Теляковского.
Задача 1.
Вычислить:
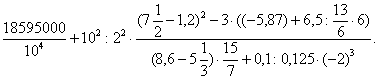
Задача 2.
Заполните таблицу, вставляя в ее пустые клетки подходящие числа:
|
a |
6 |
6 |
|
0 |
0 |
|
b |
2 |
3 |
3 |
|
|
|
c |
3 |
3 |
|
2 |
0 |
|
d |
2 |
|
0 |
|
|
|
a/b - c×d |
|
2 |
|
6 |
|
Задача 3.
В
выражении ![]() можно расставлять скобки произвольным
образом (например,
можно расставлять скобки произвольным
образом (например, ![]() или
или ![]() и т.п.). Найдите все возможные значения
для a и b, при которых независимо от расстановки скобок
в данном выражении будет получаться одно и тоже число. Чему оно равно
?
и т.п.). Найдите все возможные значения
для a и b, при которых независимо от расстановки скобок
в данном выражении будет получаться одно и тоже число. Чему оно равно
?
Следует помнить, что при решении уравнений, содержащих знак модуля, от знака модуля удобно избавляться по правилу: если а ³ 0, то ½а½ = а, а если а < 0, то ½а½= –а.
Задача 4.
Решите уравнения:
а)
![]() ; б)
; б)![]() .
.
Тема 1. Делимость целых чисел.
Числа 0; 1; -1; 2; -2; 3; -3 … называются целыми, а числа 1; 2; 3… – натуральными. Пусть a и d – целые числа, где d ¹ 0. Говорят, что число а делится на число d (пишут a M d) или число d делит число a (пишут d½a), если существует такое целое число c, что a=d·c. Известно, что если d½a и d½b, то d½(a+b) и d½(a-b). Докажите это. Повторите определения простых и составных натуральных чисел. Имеет место
Основная теорема арифметики. Всякое натуральное число, отличное от 1, разлагается в произведение простых чисел и притом единственным образом.
Так, например, ввиду 360 = 2·2·2·3·3·5, как бы мы не раскладывали 360 в произведение простых чисел, в любое такое разложение будут входить три двойки, две тройки и одна пятерка, причем другие простые числа в разложение числа 360 не будут входить. В частности, для натурального d имеем d½360 в том и только в том случае, когда в разложение d входят не более трех двоек, двух троек, и одной пятерки.
Упражнение 1. Верно ли, что если натуральное число делится на a и на b, то оно делится и на a·b, если:
а) a=6, b=10; б) a=5, b=12?
Решение. а) Неверно, так как, например, 30M 6 и 30M 10, но 60 не делит 30.
б) Верно, так как в разложение этого числа должны по крайней мере входить две двойки иодна тройка (оно делится на 12), а также – пятерка (оно делится на 5). Поэтому это число делится на 2·2·3·5=60.
Задача 5. Известно, что a, b, c, d и f – целые числа, для которых верно: 5½a, 3 не делит b, c – четное, 5½7d и 6½9f. Верно ли, что:
а) 5½3a; б) 6½2b; в) 10½5c; г) 5½d; д) f – нечетное?
Задача 6.
У Вовочки было 14 монет достоинством в один, два и пять рублей, общей суммой не более 20 рублей. Маме он сказал, что потратил все деньги на покупку жевательных резинок по цене 3 рубля за каждую.
Правду ли он сказал?
Задача 7.
Ваня и Петя купили на день рождения Маши цветы, Ваня – букет красных гвоздик по 15 рублей за каждую, а Петя – букет белых гвоздик по 25 рублей за каждую. Вместе они заплатили 200 рублей. Сколько красных и белых гвоздик купили ребята?
Повторите определения НОД и НОК натуральных чисел. Определим эти понятия для целых чисел. Пусть a и b– целые числа, из которых хотя бы одно не равняется нулю. Наибольшим общим делителем этих a и b (обозначается (a;b) или НОД(a;b)) называется наибольшее натуральное число, которое делит a и делит b. Пусть c и d – ненулевые целые числа. Наименьшим общим кратным этих чисел (обозначается [c;d] или НОК(c;d)) называется наименьшее натуральное число, которое делится на c и делится на d.
Упражнение 2. Найдите (a;b) и [a;b]:
а) a=1260, b=–1650; б) a=–90, b=539.
Решение:
а) Так как а=2·2·3·3·5·7 и │b│ = 2·3·5·5·11, то (a;b)=2·3·5=30 (общая часть разложений │a│ и │b│) и[a;b]=2·2·3·3·5·5·7·11=69300 (объединение разложений │a│ и │b│)
б) Так как │a│=2·3·3·5 и b=7·7·11, то [a;b]=2·3·3·5·7·7·11=48510 и (a;b)=1.
Для любых ненулевых целых чисел a и b справедливо равенство (a;b)·[a;b]=│a·b│ (попытайтесь его доказать, используя основную теорему арифметики). Целые числа a и b называют взаимно простыми, если (a;b)=1. Докажите для ненулевых взаимно простых чисел a и b справедливость утверждений: [a;b]=│a·b│ и, если a│c и b│c, то (ab)│c.
Задача 8.
Укажите все целые числа a и b такие, что:
а) (a;b)=[a;b] и│a│< 3;
б) (a;b)+[a;b]<3;
в) (a;b)·[a;b]=6.
Известно, что для любых целых чисел a и d, где d ¹ 0, найдется и притом единственная пара целых чисел q и r такая, что a = dq + r и 0≤r<│d│. Числа q и r называют соответственно частным и остатком при делении a на d. Докажите, что (a;d)=(d;r). Целые числа a и b, имеющие равные остатки при делении на d, называют равноостаточными. Наименьшее по модулю число b, равноостаточное с a при делении на d, можно выбрать среди двух чисел r и r–│d│.
Упражнение 3. Найдите частное q, остаток r и наименьшее по модулю равноостаточное с a число b при делении a на d:
а) a=1650, d=–105 б) a= –539, d=90.
Решение:
а) При делении “уголком” a на │d│ получим 1650=105·15+75.
Откуда 1650=(–105)·(–15)+75 и поэтому q= –15, r=75. Среди чисел 75 и
75–105= –30 наименьшим по модулю будет число –30, а, значит, b= –30.
б) При делении “уголком” │a│ на d получим 539=90·5+89. Откуда следует
–539=90·(–5)–89=90·(–5)–90+90–89=90·(–6)+1, поэтому q= –6 и r=1 (остаток должен быть неотрицательным!). Далее, из чисел 1 и 1–90 = –89 выбираем b=1.
Задача 9.
Заполните подходящими целыми числами пустые клетки таблицы:
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a |
1 |
0 |
4 |
5 |
189 |
-123 |
-225 |
-56 |
|
|
|
b |
0 |
2 |
3 |
6 |
-35 |
15 |
-24 |
|
25 |
15 |
|
(a;b) |
|
|
|
|
|
|
|
7 |
5 |
|
|
[a;b] |
|
|
|
|
|
|
|
168 |
175 |
1605 |
|
q |
|
|
|
|
|
|
|
>0 |
|
|
|
r |
|
|
|
|
|
|
|
|
|
9 |
|
c |
|
|
|
|
|
|
|
|
-10 |
|
где q и r - соответственно частное и остаток при делении a на b, с - наименьшее по модулю целое число, равноостаточное с a при делении на b.
Указание. Для решения номеров 8-10 помогут равенства (a;b)×[a;b]=ïa×bï и(a;b)=(b;r).
Определенный интерес представляют следующие утверждения, на которые можно ссылаться без их доказательств:
Утверждение 1. Остаток при делении числа на 2 (на 5) равен остатку при делении на 2 (на 5) его последней цифры;
Утверждение 2. Остаток при делении числа на 4 (на 25) равен остатку при делении на 4 (на 25) числа, составленного из двух последних цифр данного числа;
Утверждение 3. Остаток при делении числа на 3 (на 9) равен остатку при делении на 3 (на 9) числа, равного сумме цифр данного числа.
Задача 10.
Найдите наименьшее по модулю число, равноостаточное при делении на n с числом, записанным с помощью двадцати единиц и двадцати пятерок, если:
а) n=3; б) n=9; в) n=4.
Тема 2. Простейшие свойства геометрических фигур.
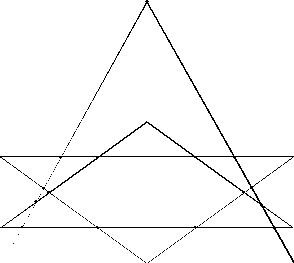
Упражнение 4. На плоскости расположены два треугольника и две прямые. Определите наибольшее возможное число точек пересечения всех прямых и сторон треугольников.
|
|
Решение. Две прямые имеют не более одной точки пересечения, отрезок или прямая имеют не более двух точек пересечения со сторонами треугольника. Так как один треугольник состоит из трех отрезков, то его стороны имеют не более 6 точек пересечения со сторонами другого треугольника. Таким образом, число точек пересечения не превосходит суммы чисел точек пересечений двух прямых, сторон треугольников, одной и другой прямой со сторонами двух треугольников, т.е. числа 1+6+4+4=15. На рисунке изображен случай, когда получается ровно 15 точек пересечений. Поэтому ответ: 15.
Задача 11.
На плоскости расположено n прямых. Как расположить 7 точек, не лежащих на этих прямых, чтобы получилось наибольшее возможное число пересечений данных прямых с отрезками, имеющими концы в этих точках, если: а) n=1; б) n=2?
Известно следующее утверждение (попытайтесь его обосновать!): если k прямых разбили плоскость на несколько частей, то (k+1)-я прямая может добавить к этим частям не более (k+1)-ой новой части; причем добавится ровно (k+1) часть лишь в том случае, когда (k+1)-ая прямая пересечет каждую из этих k прямых в точках, отличных от их точек пересечений.
Задача 12.
Используя указанное утверждение, определите, на какое наибольшее число частей могут разбить плоскость: а) 3 прямых; б) 7 прямых; в) n прямых?
Задача 13.
Определите наименьшее возможное число прямых, которые могут разбить плоскость на 20 частей. Ответ обосновать.
|
|
Задача 14.
По рисункам 1 и 2 определите углы (ab) и (cd).
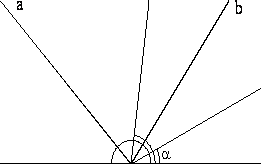
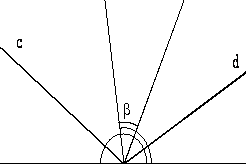
Рис.1 Pис.2
Указание. Ответы должны быть записаны с использованием букв a и b. Равные углы на рисунках отмечены одинаково.