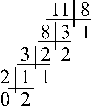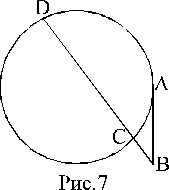Тема3. Принцип Дирихле.

 

Принцип Дирихле (П.Г.Дирихле (1805-1859) - немецкий математик) иногда называют принципом ящиков, суть его такова: если в n ящиках находится не менее  предметов, где , то в каком-то из ящиков находится не менее  предметов. Если же в n ящиках находится ровно  предметов, то в каком-то ящике не менее k предметов.

 

Упражнение 1. Имеется 1997 шаров. Какое максимальное число ящиков нужно иметь, чтобы при любом распределении этих шаров по ящикам наверняка можно было бы утверждать, что имеется ящик с не менее, чем 55 шарами ?

Решение. Искомое число n должно удовлетворять равенству , где . Откуда в силу  получаем n = 36. Поэтому достаточно иметь 36 ящиков. В 37 ящиках уже можно разместить эти шары так, что в каждом будет меньше 55 шаров.

Следующая задача на принцип Дирихле составлена по мотивам известной задачи для школьников, предложенной в 1959 году выдающимся русским математиком А.Н.Колмогоровым (1903-1987).

 

Задача1. Имеется лес елей, на каждой из которых не более 500000 иголок.

а) Докажите, что по крайней мере у двух елей равное количество игл, если в лесу 800000 елей.

б) Каково должно быть минимальное число елей в лесу, чтобы быть уверенным, что три ели имеют одинаковое число игл ?

 

Упражнение 2. В Краснодарском крае живут не менее пяти миллионов человек в возрасте от 1 до 100 лет. Можно ли среди них найти 6 человек, родившихся в один год, в один день и в один час ?

Решение. В каждом году не более 366 дней, а в каждом дне по 24 часа. Поэтому в 100 годах не более  часов. Так как , то по принципу Дирихле в один год, в один день и в один час родились по крайней мере 6 человек.

 

Задача 2. а) В квадрат со стороной 1 м. бросили произвольным образом 37 точек. Сколько из этих точек независимо от броска всегда можно накрыть квадратом со стороной 0.2 м.? Ответ обосновать.

б) Сколько точек надо произвольным образом бросить в квадрат со стороной 1 м., чтобы всегда какие-нибудь 100 из них можно было бы накрыть квадратом со стороной 0.1 м.? Укажите с обоснованием наименьшее возможное по Вашему мнению такое число точек.

 

 

Тема4. Числовые сравнения.

 

Если  целые числа a и b таковы, что  делится нацело на натуральное число m, то говорят, что a сравнимо с b по модулю m и пишут . Ясно, что a и b сравнимы по модулю m тогда и только тогда, когда они имеют равные остатки при делении на m, в частности, , если r-остаток при делении a на m, и , если m½b. Так как целое число a можно представить в виде , где ,  и q, r, - целые числа, то каждое целое число сравнимо по модулю m с одним из чисел 0,1,2,...,(m-1).

Основные свойства сравнений напоминают свойства числовых равенств: сравнения можно почленно складывать, вычитать и умножать, т.е., если  и , то , ,  (докажите эти свойства!). Для любого натурального n и целого c из того, что , следует  и . Заметим, что сокращать на d сравнение  без проверки можно лишь при взаимной простоте чисел d и m.

 

Задача 3. Докажите, что если целые числа a и m взаимно просты, то существует такое натуральное число n, что , т.е. при натуральном m имеем .

 

Указание. Рассмотреть остатки при делении чисел , , ,...,  на m и применить принцип Дирихле. Справедлива теорема Ферма (П.Ферма (1601-1665) – французский математик): если простое число p не делит нацело целое число a, то .

Упражнение 3. Найти остаток при делении  на 1997.

Решение. Учитывая, что  и 1997- простое число, не делящее 3, согласно теореме Ферма, получаем:  Так как , то 81–искомый остаток.

 

Задача 4. Найдите две последние цифры числа .

 

Упражнение 4. Доказать, что при любом целом  выражение  делится нацело на 7.

Доказательство.

Имеем: .

 

Задача 5. Докажите, что при любом натуральном n число  делится на 57.

 

Упражнение 5. Найдите все целые числа n, для которых - целое число.

Решение. Необходимо и достаточно, чтобы . Так как (2;59)=1, то, перенося 5 в правую часть и умножив на 2 обе части, получаем равносильное сравнение: , т.е. . Но (–5;59)=1 и поэтому, сокращая последнее сравнение на –5, находим , окончательно n=–2+59t, где t–любое число.

 

Задача 6. Найдите все целые числа n, для которых:

а) -целое число;

б) .

 

Тема5. Алгоритм Евклида и линейные диофантовы уравнения.

 

Алгоритм Евклида состоит в следующем: пусть a и b - целые числа (). Делим a на b, находим частное  и остаток ; если , то делим b на , находим частное  и остаток ; если , то делим  на , находим частное  и остаток . Этот процесс продолжается до тех пор, пока какой-то  разделится нацело на ненулевой остаток . Число n в этом случае называют длиной алгоритма Евклида для чисел a и b.

 

Задача 7. а) Определите длину алгоритма Евклида для чисел 1997 и 300.  б) Найдите  пару чисел, для которых длина алгоритма Евклида равна 10.

 

Имеет место утверждение: если x=y×z+t, где x, y, z, t - целые числа (), то НОД(x;y)=НОД(y;t). Действительно, полагая m=НОД(x;y) и n=НОД(x;t) из равенства получим, что m½t, т.е. , и n½x, т.е. , поэтому m=n (более подробно докажите самостоятельно). В алгоритме Евклида для a и b имеем равенства: (*) , , ,..., , . Согласно утверждению имеем НОД(a;b)=НОД(b;)=НОД()=...=НОД()=. Поэтому НОД(a;b) - это последний ненулевой остаток  в алгоритме Евклида для чисел a и b. Говорят, что целое число f является линейным выражением целых чисел g и h, если имеются целые числа u и v такие, что f=gu+hv. Перепишем равенства (*) в виде: , ,..., , . Из первого равенства линейно выражаем  через  и ; далее, подставляя вместо  правую часть второго равенства, найдем линейное выражение  через  и . Продолжая этот процесс в конце концов найдем линейное выражение  через a и b, т.е. найдем такие целые числа u и v, что НОД(а;b)=au+bv.

 

Упражнение 6.  а) Найти линейное выражение НОД(11;8).

б) Доказать, что целые числа a и b взаимно просты тогда и только тогда, когда для некоторых целых u, v имеем au+bv=1.

Решение. а) Ясно, что НОД(11;8)=1. Найдем теперь его с помощью алгоритма Евклида.      Вычисления удобно проводить “уголком“ (см. справа). Получаем 11=8×1+3; 8=3×2+2; 3=2×1+1, т.е. 1- последний ненулевой остаток в алгоритме Евклида. Теперь перепишем эти равенства в виде: 1=3–2×1; 2=8–3×2; 3=11–8×1. Откуда 1=3–2=3–(8–3×2)=–8+(11–8)×3=11×3+8×(–4).

б) С одной стороны алгоритм Евклида обеспечивает существование целых чисел u и v таких, что au+bv=НОД(a;b)=1. С другой стороны, при au+bv=1 НОД(a;b) делит нацело левую часть равенства, а, значит, делит нацело 1 и поэтому равен 1.

 

Задача 8. Пусть a, b, c - целые числа ( или ), причем НОД(a;b)=d. Доказать, что:

а) уравнение ax+by=c имеет целочисленное решение () тогда и только тогда, когда d½с;

б) если () - целочисленное решение уравнения ax+by=c при d=1, то все целочисленные решения этого уравнения имеют вид (), где t - любое целое число.

 

Уравнение с целыми коэффициентами вида ax+by=c, которое решают в целых числах, называется линейным диофантовым уравнением с двумя неизвестными x и y. Дайте определения линейных диофантовых уравнений с тремя и более неизвестными!

Упражнение 7.а) Решить диофантово уравнение .     б)  Найти  все  решения уравнения из

пункта а), для которых  и .  в) Имеются модели углов в 77° и 56°. Можно ли с их помощью получить угол в 3° ?

Решение. а) Так как 7=НОД(77;56) делит нацело 357, то уравнение имеет целочисленные решения. Разделим его обе части на 7 и получим равносильное уравнение 11x+8y=51. Согласно упражнению7 а) имеем:

11×3+8×(–4)=1, а, значит, 11×153+8×(–204)=51, т.е.  и  - частное решение уравнения. Так как НОД(11;8)=1, то согласно задаче 8 б) находим все решения: (153+8t; –204–11t), где t - произвольное целое число.

б) В силу  и  из а) имеем  и , т.е.  и t=–19. Откуда находим x=1 и y=5 - единственное подходящее решение.

в) Согласно б) имеем 77°+56°×5=357°, т.е. откладывая от данной вершины угол 77°, а затем еще 5 раз угол 56°, мы получим угол в 357°, который на 3° меньше угла в 360°. Далее очевидно.

 

Задача 9. а) Решите диофантово уравнение 14x–46y=72. 

б) Найдите натуральные числа x и y, для которых  и x+y принимает наименьшее возможное значение.

 

Задача 10. В мешке у нищенки Лисы Алисы не менее 250 купюр по 200 рублей и не менее 100 купюр по 500 рублей. Определите число способов, с помощью которых она может этими купюрами разменять 50000 рублей (только без обмана!).

 

Тема 6.  Окружность и углы,  подобие треугольников.

 

Следующие две задачи предлагаются для закрепления материала по геометрии, изложенного в теме 2 задания №1.

 

Задача 11. Из точки М внутри окружности с центром О проведены два луча, пересекающие окружность в точках А и В, причем лучи МА и МВ расположены по одну сторону от прямой ОМ и образуют с ней углы по 30°. Найдите градусную величину меньшей дуги АВ.

 

Задача 12. Два луча СА и СВ касаются окружности в точках А и В. Точка D, отличная от А и В, лежит на окружности, причем высота из вершины В треугольника DABD вдвое меньше его стороны BD. Найдите угол ÐACB.

 

Выучите определение и признаки подобия треугольников (например, из учебника А.В.Погорелова за 9-й класс или из учебника И.Ф.Шарыгина за 8-й класс). Используя эти признаки, докажите два известных утверждения, сформулированных в задаче 12.

 

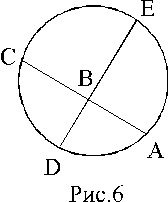
Задача 13. Доказать:

а) АВ×ВС=DB×BE

(см. рис.6);

б) АВ=ВС×BD, где АВ - касательная к окружности

(см. рис.7).

 

 

Задача 14. Хорды АВ и CD данной окружности имеют длины соответственно 4 см  и 1 см. Прямые АВ и CD пересекаются в точке М так, что АМ=2 см. Найдите длины МС и MD.