Тема 5. Комбинаторика.

 

Комбинаторика - это раздел математики, в котором в основном занимаются подсчетом числа комбинаций, составленных из определенных элементов. Рассмотрим два общих правила, с помощью которых решается большинство задач комбинаторики, - правило суммы и правило произведения.

Упражнение 1. В районной математической олимпиаде среди шестиклассников участвовало 7 девочек и 18 мальчиков.Сколько существует различных вариантов для занятия первого места в этом соревновании?

Решение. Девочку можно выбрать из всех шестиклассников 7 способами (n=7), а мальчика - 18 способами (m=18). Выбрать одного ученика (либо девочку, либо мальчика) можно n+m=7+18=25 способами.

Здесь и в аналогичных задачах используется правило суммы: если объект А можно выбрать n способами, а объект B - m способами (не такими, как объект А), то выбрать либо А, либо B можно (m+n) способами.

 

Задача 1.  Разноцветные шарики распределили по трем ящикам. В одном оказалось 6 шариков, в другом - 9, а в третьем - 2. Сколькими разными способами можно выбрать из какого-нибудь ящика один шарик?

 

Задача 2. Игрок сначала бросает белую игральную кость, потом черную. Сколько может быть случаев, когда число очков, появившихся на белой кости, больше числа очков, появившихся на черной кости?

 

Упражнение 2. В математическом кружке 8 мальчиков и 3 девочки. Для участия в зимней математической школе нужно из кружка направить одного мальчика и одну девочку. Сколько можно составить различных пар.

Решение. Мальчика из состава кружка можно выбрать 8 способами (n=8), а девочку, если мальчик уже выбран, 3 способами (m=3), т.е. на каждый способ из 8 выбора мальчика находится 3 способа выбора девочки. Поэтому таких пар можно составить m×n=8×3=24.

Здесь использовалось правило произведения: если объект А можно выбрать n способами и на каждый способ выбора объекта А существует m способов выбора объекта B, то пары объектов А и B можно выбрать n×m способам.

 

Задача 3. На должность генерального директора фирмы и его заместителя претендуют 9 человек. Сколькими различными способами  можно выбрать такую руководящую двойку?

 

Задача 4. К продаже предлагаются 3 алых, 2 белых и 4 чайных розы. Определите, сколько существует вариантов покупки: а) алой и белой роз вместе; б) двух роз различных цветов; в) трех роз различных цветов ?

 

Пусть n - натуральное число. Математики ввели специальное обозначение для произведения 1×2×3×¼×n. Такое произведение называется факториалом числа n и обозначается n! (читается : “эн факториал”). Принято считать, что 0!=1.

Упражнение 3. а) Определить, чему равны 1!, 2!, 5! и 6!/6. б) Упростить выражения 5!/3!, 1997!/1996!, n!(n+1)(n+2) и (n+1)!/(n+1).

Решение. а)1!=1; 2!=1×2=2; 5!=1×2×3×4×5=120; 6!/6=1×2×3×4×5×6/6=5!=120. б)5!/3!=(1×2×3×4×5)/(1×2×3)=4×5=20; 1997!/1996!=(1×2×¼×1996×1997)/(1×2×¼×1996)=1997; n!(n+1)(n+2)=1×2×¼×n(n+1)(n+2)=(n+2)!; (n+1)!/(n+1)=(1×2×¼×n(n+1))/(n+1)=1×2×¼×n=n!;

 

Задача 5. а) Вычислить 2×7!/3!+6!/2!-2×4!+5!/4!. б) Упростить выражения (n-1)!n(n+1)(n+2), (n+1)!/(n(n+1)) и (n+1)!/n!-n!/(n-1)!.

 

Подсчитаем теперь число способов, которыми можно расположить в ряд n предметов. Такие расположения называются перестановками.

Упражнение 4. Сколькими способами можно выложить в ряд пять разноцветных кубиков?

Решение. На первое месте можно положить любой из пяти кубиков, на второе - любой из четырех оставшихся, на третье - любой из трех оставшихся, на четвертое - любой из двух оставшихся, а на пятое место - последний оставшийся кубик. Всего получится 5×4×3×2×1=5! способа (попробуйте это самостоятельно более подробно объяснить, используя правило произведения).

Для решения подобных задач можно пользоваться следующим правилом: n различных предметов можно выложить в ряд n(n-1)×¼×2×1 различными способами, т. е. число перестановок n предметов равно n!.

 

Задача 6. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3 и 4, если каждую цифру можно использовать: а) только один раз; б) любое число раз?

 

Задача 7. На диске секретного замка от сейфа  нанесены знаки #, $, &,@ и %, а секретный код состоит из трех знаков. Какое наибольшее возможное число неудачных попыток открытия сейфа может сделать человек, не знающий кода, если : а) ни один знак кода не повторяется;  б) знаки кода могут повторяться ?

 

Задача 8. Сколько различных слов (даже бессмысленных) можно получить, переставив буквы в слове:  а) ДОСКА; б) ПАРТА?

 

 

 

Тема 6. Элементарные построения циркулем и линейкой.

 

 

 

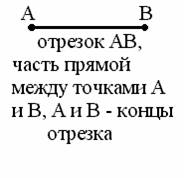
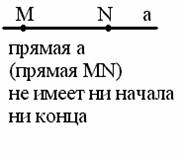
Геометрия зародилась в глубокой древности, она изучает форму и взаимное расположение фигур в пространстве, которое нас окружает. Рассмотрим простейшие фигуры и их обозначения.

В геометрии, как правило, точными считаются построения, выполненные с помощью циркуля и линейки. Эта традиция восходит к глубокой древности. Знаменитая геометрия Евклида (Евклид - древнегреческий ученый, 3-й век до н. э.) была основана на геометрических построениях, выполненных циркулем линейкой (без делений). Такой линейкой можно лишь проводить прямые линии (произвольные, через точку, через две точки). Нельзя откладывать отрезки данной длины, пользоваться обоими краями линейки. Циркулем можно строить окружности, сравнивать или откладывать данные отрезки на прямой. С  элементарными построениями циркулем и линейкой можно ознакомиться в учебнике И.Ф. Шарыгина и Л.Н. Ерганжиевой “Наглядная геометрия” (для 5-6 классов, М:1995. Параграфы 1,3,7,13).

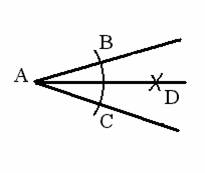
Упражнение 5. С помощью циркуля и линейки постройте луч, выходящий из вершины данного угла (см. рис.) и делящий угол пополам (этот луч называется биссектрисой угла).

Построение. Пусть А - вершина данного угла. С центром в А строим окружность. Обозначим через В и С точки пересечения окружности со сторонами угла. Из центров В и С одним и тем же радиусом строим две D пересекающиеся в какой-то точке D дуги. Тогда луч АD - биссектриса.

Повторите тему измерения углов с помощью транспортира. Угол в 90° называют прямым, меньший 90° - острым, больший 90° и меньший 180° - тупым, равный 180° - развернутым.

 

Задача 9. С помощью циркуля и линейки постройте биссектрису развернутого угла. Какие углы получаются в результате построения? Построение опишите.

 

Задача 10. Пользуясь транспортиром постройте угол в 54°, затем постройте с помощью циркуля и линейки 1/3 этого угла. Построение опишите.

 

Указание: дополните этот угол до прямого. Задача, в которой требуется разделить данный угол (с неизвестной градусной мерой) на три равных угла - классическая задача древности. Оказывается она не имеет решения, т. е. с помощью циркуля и линейки нельзя данный угол разделить на три равных угла. Это было доказано математиком П. Ванцелем в 1837 году.

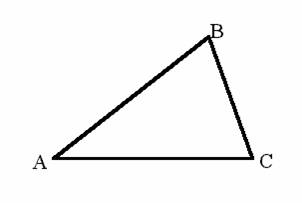
Из простейших фигур можно конструировать более сложные. Например, если три точки А, В и С не лежат на одной прямой, то общая часть углов АВС и АСВ (и ВАС) образует новую фигуру, называемую треугольником АВС (А, В и С называют вершинами, отрезки АВ, ВС и АС - сторонами, а углы АВС, АСВ и ВАС - внутренними углами этого треугольники (см. рис.)). В любом треугольнике сумма градусных величин внутренних углов равна 180°. Если все стороны треугольника равны, то его называют равносторонним  или правильным, у него внутренние углы равны по 60° .

Упражнение 6. С помощью циркуля и линейки постройте правильный треугольник, у которого длина стороны равна длине данного отрезка АВ,

где

 

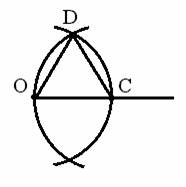
Решение. Из точки О проводим  луч, на котором с помощью циркуля откладываем отрезок ОС, равный по длине отрезку АВ. Затем с центрами О и С проводим две окружности радиуса равным длине отрезка АВ. Одну из точек пересечения этих окружностей обозначим D. Линейкой через точки О и С, С и D, O и D проведем прямые. Тогда ОСD - треугольник, который нам необходимо было построить.

Замечание: в этом упражнении мы научились строить угол в 60°.

 

 

Задача 11. Построить с помощью циркуля и линейки углы в 150° и 105°.

Правильные треугольники, соединяясь друг с другом, образуют правильный шестиугольник (см. рис.). Общая вершина треугольника - центр окружности с радиусом, равным стороне треугольника. Другими словами, правильный шестиугольник можно вписать окружность и все его стороны равны радиусу этой окружности. Попробуйте самостоятельно построить правильный шестиугольник с данной стороной циркулем и линейкой.

 

Задача 12. Перед началом математического боя жюри оценивало эмблемы команд - участников. Победила эмблема с изображением двух правильных треугольников, пересечением которых был правильный шестиугольник. Ребята нарисовали ее только с помощью циркуля и линейки. Повторите это построение и опишите его.

 

Задача 13. Отметьте на тетрадном листе две точки А и В. Они будут являться концами отрезка. Пользуясь только циркулем, постройте концы отрезка, вдвое длиннее отрезка АВ.

 

Если в треугольнике две стороны равны, то его называют равнобедренным, эти стороны - боковыми, а третью сторону - основанием. В таком треугольнике углы при основании равны.

 

Задача 14. Не проводя биссектрису, циркулем и линейкой постройте угол меньший данного угла.