Тема 3. Сравнения и их применение к

решению задач.

 

Если целые числа а и b равноостаточны при делении на натуральное число d, то обычно пишут или кратко  (читается: “a сравнимо с b по модулю d”). Если r- остаток при делении а на d, то имеет аºr(mod d). Объясните равносильность высказываний: d½a  и аº0(mod d). Известно одно важнейшее свойство  равноостаточных  чисел: если аºb(mod d)  и cºf(mod d), то а+сºb+f(mod d), a-cºb-f(mod d) и a×cºb×f(mod d). Попробуйте самостоятельно доказать это свойство.

Упражнение 1. Равноостаточны ли при делении на 1997 числа  и ?

Решение. При d = 1997 получаем 2000º 3, 3995º 1, 1999º 2, 1996º -1, 2050º 53, 1998º 1 и по свойству равноостаточных чисел данные два числа равноостаточны с числами  и . Таким образом, числа равноостаточны.

 

Задача 1. Найдите последнюю цифру числа ?

 

Указание: последняя цифра равна наименьшому неотрицательному  целому числу, равноостаточному с данным числом при делении на 10.

Упражнение 2. Найти остаток при делении на 9 числа а, где а - число, записанное с помощьб цифр 0, 1, 2, 3 и 4, каждая из которых встречается в записи ровно 20 раз.

Решение. По правилу нахождения остатка число а равноостаточно с числом 20×0+20×1+20×2+20×3+20×4=200, т. е. с числом 2. Откуда . Замечаем, что   и 1997=6×332+5, поэтому , т. е. искомый остаток равен 5.

Заметим, что часть рассуждений в ходе решения можно было провести иначе. В последовательности наименьших по модулю чисел, равноостаточных с числами 2, ,,,¼, имеется определенная закономерность: , , , , , , , , , , ,  и т. д. Мы видим периодическую последовательность чисел: 2, 4, -1, -2, -4, 1, 2, 4, -1, -2, -4, 1, ¼ . В этой последовательности чисел находим 1997-й член. Так как 1997 = 6×332 + 5, то сначала встречаем 332 раза набор чисел 2, 4, -1, -2, -4, 1, а затем еще пять чисел из этого набора, т. е. 1997-й член будет число -4, равноостаточное с 5.

 

Задача 2. Найдите две последние цифры числа .

 

Упражнение 3. Пусть  - десятичная запись натурального числа n. Докажите, что числа n и  - равноостаточны при делении на 11.

Доказательство. Замечаем, что , откуда получаем:

 .

Указанное в упражнении 3 правило нахождения остатка при делении на 11 можно использовать при олимпиадных задач без доказательств. В первой части заочной школы были сформулированы другие правила нахождения остатков при делении на числа: 2, 5, 4, 25, 3 и 9. Теперь попробуйте доказать эти правила, используя свойство равноостаточных чисел.

 

Задача 3. Сформулируйте и обоснуйте правило, по которому, зная десятичную запись числа n , мы сможем найти натуральное число не более 63, равноостаточное с n при делении на 8.

 

Задача 4.

а) Может ли число, записанное с помощью цифр 0, 1, ¼ , 9, каждая из которых встречается в его десятичной записи по 1997 раз, делится нацело на 11 ?

б) Найдите наименьшее натуральное число, равноостаточное при делении на 11 с числом , где  ( в записи а цифры 1 и 7 встречаются по 1000 раз, а 9 - 2000 раз).

 

Для любого натурального m среди любых m последовательных чисел всякие два имеют разные остатки при делении на m, т.е. их остатки с точностью до порядка следования равны 0, 1, 2, ¼ , m - 1. В частности, одно из этих чисел делится нацело на m.

Упражнение 4. Докажите для любого целого m, что число а кратно числу b:

а) а = m×(m+1)×(m+2)×¼×(m+8)  и b = 362880;

б)  и  b = 5.

Доказательство.

а) Среди восьми последовательных чисел m, m+1, m+2, ¼ , m+7 найдем числа с остатками 0, 2, 4 и 6 при делении на 8, поэтому число а делится на 9, а значит число а делится на 9×3×3 = 81. Среди первых пяти чисел найдем число, делящееся на 5, а среди первых семи - число, делящееся на 7. Учитывая, что числа 128, 81, 5 и 7 - попарно взаимно простые, получаем, что а делится на 128×81×5×7 = 362880.

m	0	1	2	3	4
	0	1	4	4	1
	0	1	3	2	4
	0	1	1	1	1

б) Из таблицы замечаем, что  при  и  при . Откуда  и . Окончательно , т.е. число а кратно 5.

 

Задача 5. Докажите, что для всех натуральных n число a кратно числу b:

а)  и b = 120;

б)  и b=7.

 

Указание: а) при делении на 120 данное число a равноостаточно с числом , которое после разложения на множители представимо в виде произведения пяти последовательных целых чисел.

При решении некоторых задач используют так называемый принцип Дирихле: если в n ящиках помещено не менее (n + 1) предметов, то в каком-то из ящиков будет не менее двух предметов. Доказательство этого принципа легко получается методом от противного: если бы в каждом ящике было не более одного предмета, то во всех ящиках было бы не более n предметов, что противоречит условию.

Упражнение 5. Докажите, что:

а) для любых (m+1) целых чисел найдется хотя бы два, разность которых делится на m, где m - натуральное число;

б) для любого натурального числа m, взаимно простого с 10, можно написать с использованием только одной цифры “1” натуральное число n, которое делится на m.

Доказательство.

а) Применим принцип Дирихле: в качестве “ящиков” рассмотрим все остатки 0,1,...,m-1 при делении на m, а в качестве “предметов” - числа этого набора из (m+1) чисел. Тогда в одном из ящиков будет по крайней мере два предмета, т.е. хотя бы два числа из данного набора равноостаточны и тогда их разность делится на m.

б) Рассмотрим (m+1) чисел вида 1; 11; 111;...; 11...1. По доказанному в пункте а) среди них найдем два числа, разность которых делится на m. Так как разность этих двух чисел имеет вид  (n записано с помощью единиц и k - некоторое натуральное число), то ввиду (10;m)=1 получаем, что m½n.

 

Задача 6. Докажите, что существует не более чем 122-значное число n, кратное 122, которое можно записать цифрами “8” и “9”, используя каждую из них одинаковое число раз в десятичной записи числа n.

 

Указание. Рассмотрите 62 числа вида 98; 9898; 989898;..., а далее как и в упражнении 5 б).

Имеет место еще обобщенный принцип Дирихле: если в n ящиках помещено не менее (k×n+1) предметов, то в каком-то ящике будет не менее (k+1) предметов. Докажите!

 

Задача 7. Имеется набор из 30 двухзначных натуральных чисел. Для каждой пары этих чисел нашли их сумму. Докажите, что среди полученных сумм будет хотя бы три равных.

 

Указание. Всего таких сумм будет 435, а каждая сумма является числом от 20 до 198.

 

 

 

Тема 4. Треугольники. Углы.

 

Задача 8. Имеется n треугольников, каждые два из которых удовлетворяют свойству: хотя бы две стороны и угол одного треугольника равны каким-то двум сторонам и углу другого треугольника.

а) Предполагая, что имеющиеся треугольники попарно не равны, определите наибольшее возможное значение для n.

б) При n=1997 докажите, что среди имеющихся треугольников найдутся не менее 500 равных друг другу.

 

Указание. а) Существуют, например, четыре попарно не равных треугольника со сторонами 3 см. и 4 см. и углом в 30°;

б) Применить обобщенный принцип Дирихле.

 

Задача 9. В равнобедренном треугольнике DАВС (АВ=ВС) тупой угол между биссектрисами углов ÐАВС и ÐВАС равен 100°. Найти внешний угол при вершине В.

 

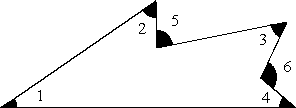
Задача 10. Используя рисунок, докажите равенство:

Ð1+Ð2+Ð3+Ð4=Ð5+Ð6.

 

 

 

 

 

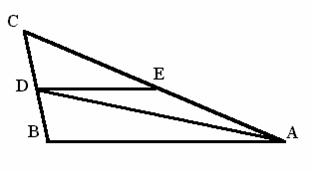
Задача 11. Используя рисунок, докажите каждое из следующих трех утверждений:

а) если ÐBAD=ÐCAD и AE=ED, то AB½½ED;

б) если AE=ED и AB½½ED, то ÐBAD=ÐCAD;

в) если AB½½ED и ÐBAD=ÐCAD, то AE=ED;

 

 

 

 

 

Большую роль при решении олимпиадных заданий по геометрии играют так называемые “неравенства в треугольнике”. Первое из них: внешний угол треугольника больше любого внутреннего угла, не смежного с ним. Второе звучит так: в треугольнике против бóльшей стороны лежит больший угол, против большего угла лежит большая сторона. Третье, называемое неравенством треугольника: в треугольнике сумма длин любых двух сторон больше длины третьей. Отметим, что первое и второе неравенства можно легко доказать. Попытайтесь это сделать! Третье неравенство (неравенство треугольника) следует из того, что кратчайшим путем между двумя точками является отрезок прямой линии. Однако, имеет место еще более сильное утверждение: из трех отрезков можно собрать треугольник тогда и только тогда, когда сумма длин любых двух из них больше длины третьего (сумма длин меньших отрезков больше  длины большего отрезка).

 

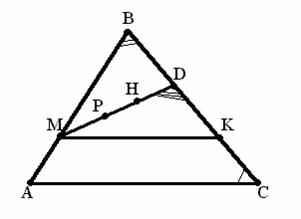
Задача 12. В треугольнике взяли две произвольные точки. Докажите, что расстояние между ними не превышает большей стороны треугольника.

 

Указание. Пусть P,H - точки в DАВС и АС - наибольшая сторона. Рассмотрим ситуацию, как указано на рисунке, и без подробных обоснований (сделайте самостоятельно!) приведем схему рассуждений: полагаем МК½½АС, тогда МК £ АС. Так как АС³АВ, то ÐВ³ÐС. Но ÐMDK>ÐB, поэтому ÐMDK>ÐC=ÐMKD, а значит MK>MD и тем более АС>MD³PH.

 

Задача 13. Внутри треугольника АВС расположена точка О. Докажите, что:

а) АО+ВО+СО больше полупериметра треугольника АВС;

б) АВ+СВ>AO+CO;

в) АО+ВО+СО меньше периметра треугольника АВС.

 

Указание. В задании б) продлить прямую АО до пересечения со стороной ВС в точке D и, используя неравенство треугольника, рассмотреть треугольники DABD и DODC.

 

Задача 14. В плоскости расположены четыре точки А, В, С и D. Длины отрезков АВ, ВС, CD, DA и АС записали в порядке возрастания и получили 3 см., 5 см., 7 см., 13 см., 19 см. Найдите длину отрезка АС. Ответ обосновать.