Задание 32.а) Найти операционным методом частное решение дифференциального уравнения , удовлетворяющее начальным условиям у(0)=0, у¢ (0)=0.

Решение.

Пусть y(t)=Y(p).

Тогда по свойству дифференцирования оригинала с учетом начальных условий имеем

По таблице .

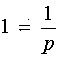Переходя в исходном дифференциальном уравнении к изображениям, получим соответствующее операторное уравнение

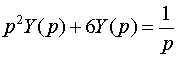из которого находим

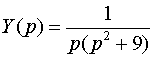Разлагая эту дробь на элементарные, получим

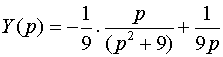Пользуясь таблицей, находим решение:

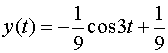Задание 32. б) Найти операционным методом частное решение дифференциального уравнения

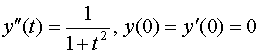удовлетворяющее начальным условиям у(0)=0, у¢ (0)=0.

Решение.

Составим вспомогательное уравнение

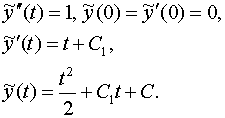
Воспользуемся начальными условиями:

Итак,

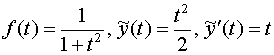Тогда

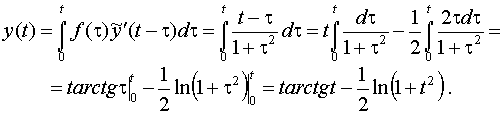
Задание 33. Найти решение уравнения

удовлетворяющее начальным условиям

Решение.

Пусть y(t)=Y(p). По свойству дифференцирования оригинала с учетом начальных условий имеем

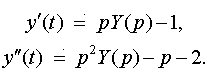
По таблице: .

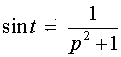Получаем соответствующее операторное уравнение

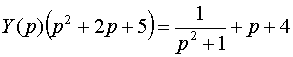Находим Y(p):

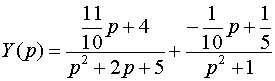или

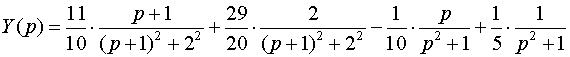Пользуясь таблицей, получим решение:

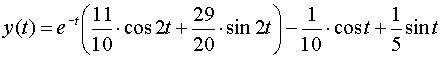2. Применение формулы Дюамеля. При решении дифференциальных уравнений иногда удобно применять формулу Дюамеля (см. задание 31, пр. 2).

Пусть требуется решить обыкновенное дифференциальное уравнение п-го порядка с постоянными коэффициентами.

при нулевых начальных условиях

где f(t) – оригинал.

(Заметим, что простой заменой искомой функции задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями.)

Рассмотрим вспомогательное линейное дифференциальное уравнение

при тех же нулевых начальных условиях.

Предположим, что известно решение этого дифференциального уравнения – , которое является оригиналом. Допустим, что искомое решение уравнения (1) – также является оригиналом.

Для изображения введенных нами оригиналов используем обозначения:

, , .

Применяя к левой и правой частям уравнений и преобразование Лапласа с учетом нулевых начальных условий, придем к операторным уравнениям

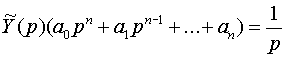Разделив первое из этих уравнений на второе, получим соотношение

Применив интеграл Дюамеля и используя свойства свертки, получим искомое решение y(t) в виде

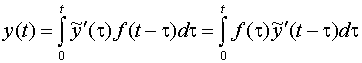
или в виде
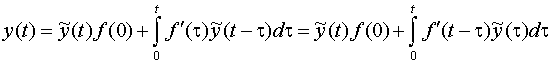