НАХОЖДЕНИЕ ОРИГИНАЛА ПО ЕГО ИЗОБРАЖЕНИЮ
Для решения задачи о нахождении оригинала f (t) по известному изображению F(p) применяются следующие приемы, используемые при выполнении задания 31:
Пример 1.
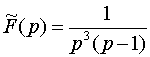 .
.
Решение. Пусть
![]() ,
,
где 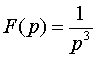 ,
а
,
а 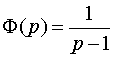 .
.
По таблице определяем оригиналы функций F(р) и Ф(р):
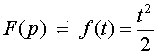 ,
,
![]() .
.
Искомый оригинал ![]() определяем
как свертку оригиналов f (t)
и j (t)
определяем
как свертку оригиналов f (t)
и j (t)
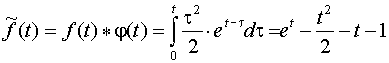 .
.
2. Применение
формулы Дюамеля. Если
функция-оригинал f (t)
непрерывна на [0,+
), а функция-оригинал j (t)
непрерывно дифференцируема на [0,+
) и
![]() ,
,
![]() ,
,
то
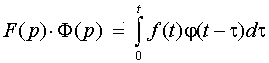 .
.
Отсюда по теореме о дифференцировании оригинала
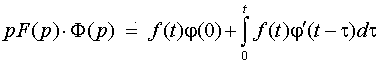 .
.
Это – так называемая формула Дюамеля.
Пример 2.
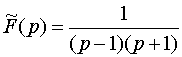 .
.
Решение. Обозначим
искомый оригинал через ![]() , т. е.
, т. е.
![]() .
.
Пусть 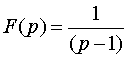 ,
а
,
а 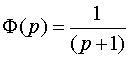 .
.
Тогда ![]() ,
а
,
а ![]() .
.
Находим ![]() ,
,
![]() и
по формуле Дюамеля имеем
и
по формуле Дюамеля имеем
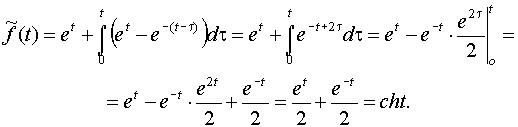
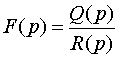
есть правильная рациональная дробь, то разлагают эту дробь на сумму простых дробей и находят оригинал для каждой простой дроби, используя свойства преобразования Лапласа.
Пример 3.
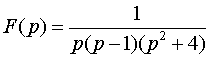 .
.
Решение. Разлагаем F(p) в сумму простых дробей:
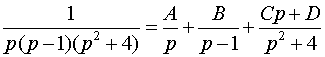 .
.
Находя коэффициенты А, В, С, D, получаем
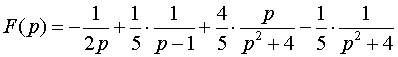 .
.
С помощью таблицы определяем
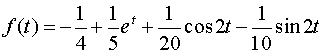 .
.
Ответ: 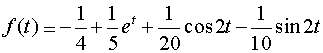 .
.
4. Применение второй теоремы разложения. Вторая теорема разложения утверждает, что при определенных условиях на F(p) оригиналом для F(p) служит функция
![]() ,
,
где сумма вычетов берется по всем особым точкам рk функции F(p).
В частности, если
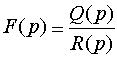
правильная рациональная дробь, то оригиналом ее служит функция
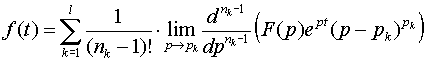 ,
(1)
,
(1)
где рk – полюсы F(p) кратности nk и сумма берется по всем полюсам F(p).
Пример 4.
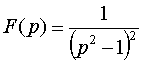 .
.
Решение. Функция F(p) имеет полюс p1=1 и p2=-1каждый второго порядка. В формуле (1) n1=2, n2=2, l=2, k=1, 2.
По формуле (1) имеем
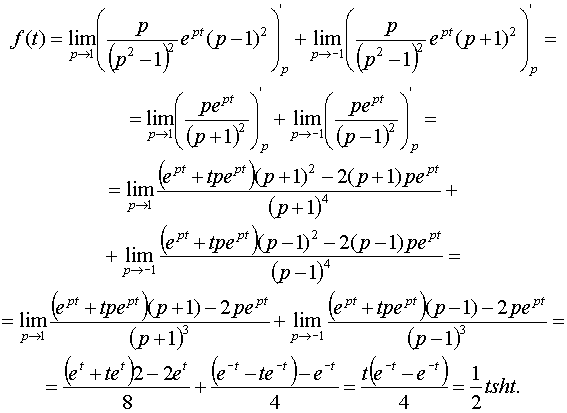
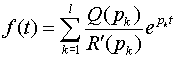 .
.
Пример 5. 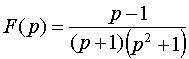 .
.
Решение. Имеем случай, когда все полюса F(p) простые:
![]() .
.
Тогда
![]() ,
,
![]() ,
,
![]() ,
,
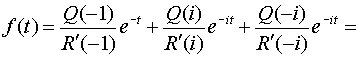
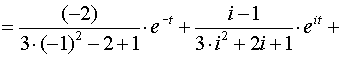
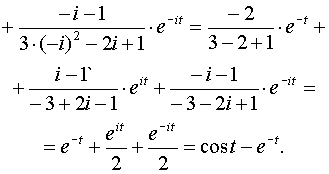
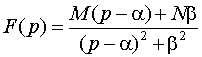 ,
,
. Пример 6.
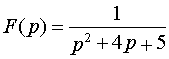 .
.
Решение. Поскольку
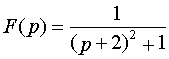 ,
,
то
![]() .
.
Имеем
![]() .
.
