Иррациональное неравенство
![]()
равносильно системе неравенств:
Иррациональное неравенство
![]()
равносильно совокупности двух систем неравенств:
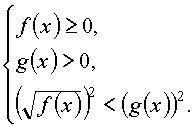
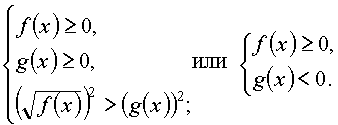
3.5 Иррациональные неравенства
Основная идея решения иррациональных неравенств, т.е. неравенств, в которых неизвестное входит под знак радикала, заключается в сведении его к равносильной системе рациональных неравенств или совокупности таких систем. При этом необходимо либо найти ОДЗ отдельно, либо включить неравенства, определяющие ОДЗ в соответствующую систему неравенств, равносильную исходному неравенству, и применять метод равносильных преобразований систем.
Обычно, при сведении к рациональному неравенству применяют правило уединения радикалов, а затем возводят обе части неравенства в натуральную степень. При этом пользуются утверждением:
@
При возведении обеих частей неравенства в нечётную, натуральную степень всегда получается неравенство равносильное исходному. Если же обе части неравенства возводить в четную степень, то равносильное исходному и имеющее тот же знак будет получаться в том случае, когда обе части неравенства неотрицательны.
В частности, имеет место утверждение:
|
Иррациональное неравенство
равносильно системе неравенств: |
Иррациональное неравенство
равносильно совокупности двух систем неравенств: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|