Пример
3.3.3. (РГУ, отделение прикладной математики, 1992 г.Решить неравенство
![]() .
.
Решение:
1-й способ.
В данном случае удобнее корни не уединять. Неравенство равносильно системе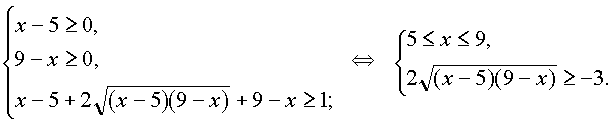
|
Однако неравенство |
|
выполняется при всех x из ОДЗ. |
|
|
Следовательно, |
|
||
2-й способ.
Воспользуемся идеями метода интервалов. ОДЗ определяется неравенством:|
|
Рассмотрим функцию |
|
Найдем её |
|
|
интервалы знакопостоянства. Для этого определим сначала её корни, т.е. решим |
||||
|
уравнение |
|
|||
Имеем, возводя обе части в квадрат,
![]() .
.
|
Уравнение решений не имеет. Таким образом, на |
|
Функция f(x) |
||||
|
сохраняет знак, при этом f(x) > 0. Следовательно, |
|
|||||
на всем промежутке.
|
Ответ: |
|