Пример
3.3.4.Решить неравенство
![]()
Решение:
ОДЗ неравенства определяется множеством тех x, для которых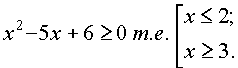
Проверкой убеждаемся, что числа х
1=3 и х2 =2 являются решениями исходного неравенства.|
Далее на оставшейся части ОДЗ, т.е. на интервалах |
|
функция |
||||||
|
|
положительна. Следовательно, на этом множестве исходное |
|||||||
|
неравенство равносильно неравенству |
|
Множество решений |
||||||
|
последнего неравенства |
|
полностью содержится в ОДЗ. Объединяя |
||||||
|
решения на всех частях ОДЗ, находим, что решение исходного неравенства состоит |
||||||||
|
из точки х=2 и промежутка |
|
|||||||