@Тела вращения и многогранники могут быть вписаны одно в другое при некоторых ограничениях.

     Призма называется вписанной в цилиндр, если ее основания – многоугольники, вписанные в окружности оснований цилиндра, а боковые ребра совпадают с образующими цилиндра.

      В цилиндр можно вписать только такую прямую призму, основания которой можно вписать в окружность.

      Призма называется описанной около цилиндра, если ее основания – многоугольники, описанные около окружностей оснований цилиндра.

      Около цилиндра можно описать только такую прямую призму, основания которой – многоугольники, которые можно описать около окружности.

      Очевидно, что у таких цилиндров и призм высоты равны.

      Призма называется вписанной в конус, если одно ее основание вписано в окружность сечения конуса плоскостью, параллельной основанию, а другое основание принадлежит основанию конуса.

      В конус можно вписать только такую прямую призму, вокруг основания которой можно описать окружность.

      Очевидно, что высота вписанной призмы меньше высоты конуса.

      Конус называется вписанным в прямую призму, если его вершина принадлежит одному основанию призмы, а основание конуса вписано в другое основание призмы.

      Конус можно вписать только в такую призму, в основание которой можно вписать окружность.

      Очевидно, что в этом случае высота конуса и высота призмы равны.

      Пирамида называется вписанной в конус, если ее ребра совпадают с образующими конуса, а основание вписано в основание конуса.

      Попробуйте доказать утверждение

      Для того, чтобы в конус можно было вписать пирамиду, необходимо и достаточно, чтобы у нее были равные боковые ребра.

      Конус называется вписанным в пирамиду, если его вершина совпадает с вершиной пирамиды, а основание вписано в основание пирамиды.

Докажите утверждение

      В пирамиду можно вписать конус тогда и только тогда, когда все апофемы боковых граней пирамиды равны.

Очевидно, что у таких конусов и пирамид высоты равны.

      Пирамида называется вписанной в цилиндр, если ее вершина принадлежит одному основанию цилиндра, а основание вписано в другое основание цилиндра.

      В цилиндр можно вписать пирамиду, основание которой можно вписать в окружность.

      Очевидно, что высота вписанной пирамиды равна высоте цилиндра.

      Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.

     В сечении пирамиды плоскостью, параллельной основанию, получается многоугольник, подобный основанию пирамиды. Следовательно, в пирамиду можно вписать цилиндр только в том случае, если в основании пирамиды – многоугольник, в который можно вписать окружность.

    Очевидно, что высота вписанного цилиндра меньше высоты пирамиды.

    Многогранник называется вписанным в сферу (шар), если все его вершины лежат на сфере. Такая сфера называется описанной около многогранника.

    Докажите утверждения

    1. Для того, чтобы около пирамиды можно было описать сферу, необходимо и достаточно, чтобы около основания пирамиды можно было описать окружность.

    2. Около любой правильной пирамиды можно описать сферу.

    3. Для того, чтобы около призмы можно было описать сферу, необходимо и достаточно, чтобы призма была прямая и около ее основания можно было описать окружность.

    4. Около любой правильной призмы можно описать сферу.

    Сфера называется вписанной в многогранник (а многогранник – описанным около сферы), если она касается всех его граней.

    Полезно уметь доказывать следующие утверждения

    1. В любую правильную пирамиду можно вписать сферу (шар).

    2. Для того, чтобы в призму можно было вписать сферу, необходимо и достаточно, чтобы в перпендикулярное сечение призмы можно было вписать окружность и чтобы высота призмы была равна диаметру этой окружности.

    3. В правильную призму можно вписать сферу тогда и только тогда, когда ее высота равна диаметру окружности, вписанной в основание.

Упражнение 7.7.1.

    1. Найти площадь основания правильной призмы, вписанной в цилиндр, радиус основания которого равен R.

    Ответ: , где n – число сторон.

    Очевидно, такой же ответ будет для правильной пирамиды, вписанной в конус.

    2. В шар радиуса R вписана правильная четырехугольная пирамида с высотой, равной Н. Как связана сторона основания пирамиды с высотой пирамиды и радиусом шара?

    Ответ: .

Пример 7.7.2. (КубГУ, матем., 1971 г.).

    В шар радиуса R вписана правильная треугольная пирамида с плоским углом a при вершине. Найти объем пирамиды, а также боковую поверхность конуса, описанного около указанной пирамиды.

Пусть сторона основания пирамиды равна a, радиус основания конуса, описанного около этой пирамиды равен r, тогда  .       Грани пирамиды – равнобедренные треугольники. Тогда DK – высота, медиана и биссектриса DABD. Из прямоугольного треугольника ADK имеем   .

, .

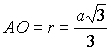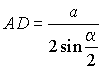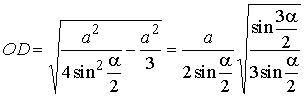      DM – диаметр шара. Тогда в сечении шара, проходящем через диаметр DM и точку А, получим прямоугольный треугольник AMD. Из метрических соотношений в прямоугольном треугольнике имеем

.

, откуда .

     Тогда площадь основания найдем по формуле 

.

      И из формулы  находим объем пирамиды

.

      Ребро AD по определению описанного конуса является его образующей. Тогда найдем боковую поверхность описанного конуса по формуле S _бок = pr1.

S _бок .

      Ответ: ; S _бок .

Пример 7.7.3. (КубГУ, матем., 1979 г.)

      В конус, образующая которого длины  наклонена к плоскости основания под углом a, вписана правильная n-угольная призма, все ребра которой имеют равные длины. Найти полную поверхность призмы.

По условию все ребра n - угольной призмы равны, следовательно, ее грани – квадраты. Пусть сторона квадрата равна a, тогда

S _бок , .

Задача свелась к нескольким планиметрическим соотношениям. Из прямоугольного треугольника АОК находим .
 

Из подобных прямоугольных треугольников АОС и  находим  , , тогда

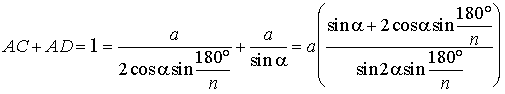, откуда

, тогда S _бок ,

.

      И окончательно

   S _п = S _бок + 2 

.

      Ответ: .

Пример 7.7.4. (КубГУ, матем., 1991 г.)

      В основании пирамиды лежит квадрат со стороной а. Высота пирамиды проходит через середину одного из ребер основания и равна . Найти радиус сферы, описанной около пирамиды.

Типичной ошибкой при решении этой задачи является утверждение о том, что центр описанной сферы находится на грани SBC. В действительности положение точки О не связано с гранью SBC.   В силу равноудаленности точки О от вершин S, A, B, C, D следует, что OABCD – правильная четырехугольная пирамида.  Следовательно, на грань ABCD точка О проектируется в точку М – точку пересечения диагоналей.

. .

, .

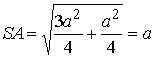      Следовательно, треугольник SAD – равносторонний и OASD – правильная треугольная пирамида. Тогда точка О проектируется на грань SAD в центр треугольника SAD . Отсюда , .

      Из треугольника SON находим искомый радиус SO

,

.

      Ответ: .