@Часто встречаются и представляют интерес задачи, в которых взаимодействуют тела вращения с телами вращения и многогранниками.

      Сфера называется описанной около цилиндра (конуса), если окружности его оснований (окружность его основания и вершина) принадлежат сфере.

      Около любого цилиндра и любого конуса можно описать сферу.

      Сфера называется вписанной в цилиндр, если она касается каждой образующей и обоих оснований цилиндра.

      В цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания.

       Центр сферы является серединой отрезка, соединяющего центры оснований.

      Сфера называется вписанной в конус, если она касается образующих конуса и его основания.

       В любой конус можно вписать сферу.

       Сфера называется вписанной в усеченный конус, если она касается всех образующих и обоих оснований конуса.

      Очевидно справедливо утверждение: в усеченный конус можно вписать сферу тогда и только тогда, когда образующая усеченного конуса равна сумме радиусов оснований. Тогда диаметр сферы равен высоте усеченного конуса.

      Понятия вписанная и описанная сферы и вписанный и описанный шары в задачах не различаются.

      Цилиндр называется вписанным в конус, если одно его основание принадлежит основанию конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию.

      Основание цилиндра и основание конуса – концентрические круги.

      Во всякий конус можно вписать цилиндр. Его высота меньше высоты конуса.

      Цилиндр называется вписанным в усеченный конус, если одно его основание принадлежит основанию конуса, а другое совпадает со вторым основанием конуса. Высота такого цилиндра равна высоте усеченного конуса.

      Так как цилиндр и конус однозначно определяются двумя независимыми параметрами, то, задав два независимых параметра одной фигуры и один параметр другой (вписанной или описанной), можно найти остальные параметры.

Упражнение 7.6.1.

      1. В конус высоты Н и радиуса R вписан цилиндр высоты h. Найти радиус основания цилиндра.

      Ответ: .

      Шар задается однозначно одним параметром, поэтому, задав параметр шара и один из независимых параметров вписанного или описанного конуса или цилиндра, можно найти другой параметр.

      Или же по двум независимым параметрам конуса или цилиндра можно определить параметр вписанного или описанного шара.

      2. В конус высоты Н и радиуса R вписан шар. Найти радиус шара.

      Ответ: .

      3. В усеченный конус, радиусы оснований которого R и r, вписан шар. Найти его радиус.

      Ответ: .

      4. В шар радиуса R вписан цилиндр высоты Н. Найти радиус его основания.

      Ответ: .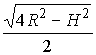

Пример 7.6.2. (КубГУ, матем., 1971 г.)

      В прямой конус с образующей 1 и углом 2a при вершине осевого сечения вписан шар. Вычислить радиус окружности, по которой соприкасаются поверхности конуса и шара, а также объем и полную поверхность меньшей из частей шара, на которые он рассекается кругом упомянутого радиуса.

      Решение задач о вписанных телах вращения, как правило, сводится к планиметрическим. Поэтому сделаем чертеж осевого сечения конуса. Тогда сфера будет окружностью большого круга, вписанной в равнобедренный треугольник. Отрезок прямой, параллельной основанию, соединяющий точки касания окружности и треугольника, будет диаметром искомой окружности.

      Из прямоугольного треугольника ACD имеем  AD = 1 sin a.

АО – биссектриса угла CAD, следовательно, .

     Из прямоугольного треугольника AOD  находим 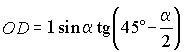, OD = OM как радиусы.

DMKO подобен DCMO, следовательно, KMO = a

и .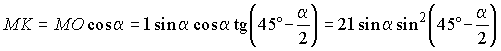
 

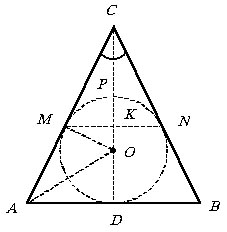МК – искомый радиус r.         Меньшая часть шара – шаровой сегмент, высота которого РК. Его объем и площадь поверхности вычисляются по формулам  , S = 2 pRH.        Тогда полная поверхность будет равна площади шарового сегмента и площади круга найденного радиуса  S п = S сегм + S кр , где S кр .

     Из треугольника МКО найдем КО

.

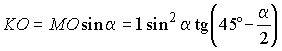      Тогда PK = PO - OK. Подставив найденные величины и преобразовав, получим

,

.

     Ответ: ;

;

.

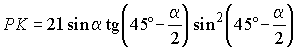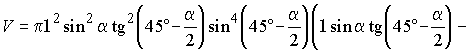
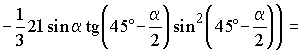
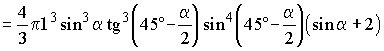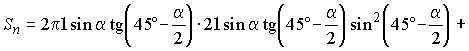
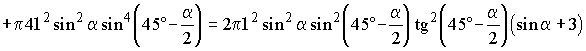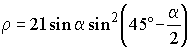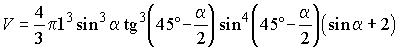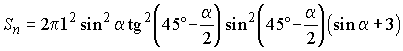Пример 7.6.3. (КубГУ, матем., 1979 г.)

      Площадь поверхности шара, вписанного в конус, равна площади основания конуса. Найти величину угла между образующей конуса и плоскостью его основания.

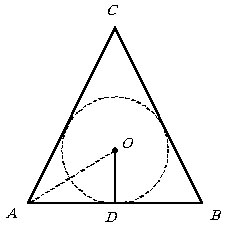Пусть r – радиус шара, R – радиус основания конуса. По условию задачи S ш = S осн. , откуда R = 2r. В осевом сечении конуса AD = R, OD = r, т.е. AD = 2 OD. Центр вписанной окружности лежит на биссектрисе АО. Тогда из прямоугольного треугольника AOD имеем  , РCAD = 2 РOAD. Следовательно, .

      Ответ: .

Пример 7.6.4. (КубГУ, матем., 1986 г.)

      В усеченный конус вписан шар, касающийся обоих оснований и боковой поверхности. Найти длину образующей усеченного конуса, если даны его высота h и радиус a окружности касания.

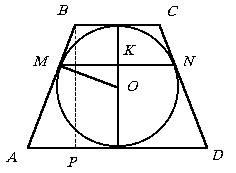Сделаем чертеж осевого сечения. Тогда MK = a, BP = h. Так как высота конуса равна диаметру шара, то 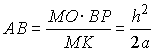. РOMK = РABP, как острые углы со взаимно перпендикулярными сторонами. Тогда  DOMK подобен DABP  и имеет место соотношение , откуда .

     Ответ: .

Пример 7.6.5. (КубГУ, эконом., 1989 г.)

      В прямой круговой конус, в котором образующая наклонена к плоскости основания под углом a, вписаны 2 шара таким образом, что один касается основания и боковой поверхности конуса, а другой – боковой поверхности конуса и первого шара. Найти отношение объемов этих шаров.

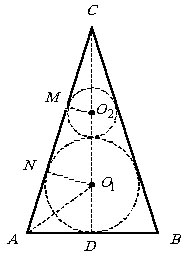Отношение объемов шаров равно отношению кубов их радиусов, т.е. 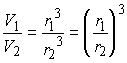.  Пусть AC = a, тогда из чертежа осевого сечения находим CD = a tg a, .  подобен DCAD (прямоугольные с общим углом при вершине С).

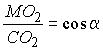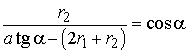Тогда  и , , откуда

.

Разделив обе части на , получим

.

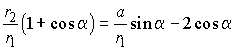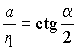      Из прямоугольного треугольника  имеем , тогда

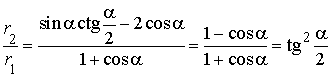, откуда

, .

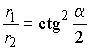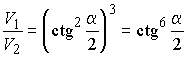      Ответ: .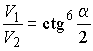

Пример 7.6.6. (КубГУ, матем., 1979 г.)

      В усеченный конус вписан шар радиуса R. Образующая конуса наклонена к плоскости нижнего основания под углом ( a < 90°) . Найти объем усеченного конуса.

      В осевом сечении получим равнобедренную трапецию с вписанной в нее окружностью большого круга.  (см. определение),  . Тогда из прямоугольного треугольника АВК находим , .
 

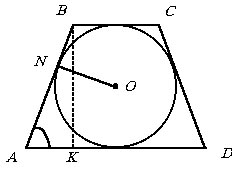Но ВК равно диаметру вписанной окружности, следовательно,  (см. упр. 3).  Из треугольника АВК имеем . Тогда .

     Подставив найденные соотношения в объем и выполнив преобразования, получим

.

      Ответ: .

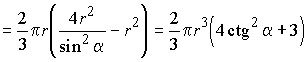Пример 7.6.7.

      В шар радиуса R вписан конус. Угол между образующей конуса и плоскостью основания равен a. В конус вписан шар. Найти радиус вписанного шара.

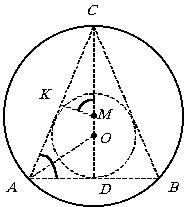
В осевом сечении конуса получили равнобедренный треугольник с вписанной и описанной окружностями. Отметим, что центры вписанной и описанной окружностей совпадают только у правильного треугольника. Если угол при вершине равнобедренного треугольника меньше 60°, то центр описанной окружности расположен на высоте ближе к этой вершине, чем центр вписанной окружности. Если треугольник прямоугольный, то центр описанной окружности совпадает с серединой гипотенузы, если же треугольник тупоугольный, то центр описанной окружности будет расположен вне треугольника, в то время как центр вписанной окружности для любого треугольника является внутренней точкой.

     Пусть М – центр описанной окружности, тогда MC = R, РCMK = РCAD = a (DCAD и DCKM подобны как прямоугольные с общим углом при вершине С).
 

Из треугольника СМК имеем CK = R sin a, AC = 2 CK = 2R sin a. Тогда из треугольника ACD находим AD = AC cos a =  R sin 2a.  Если О – центр вписанной окружности, то АО биссектриса DCAD и из треугольника OAD находим .  OD – искомый радиус.

     Ответ: .

Пример 7.6.8. (КубГУ, физич., 1979 г.)

      Шар радиуса R вписан в конус. Из центра шара образующая конуса видна под углом a. Найти объем конуса.

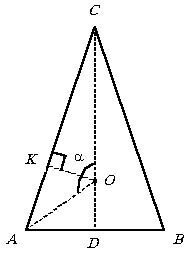Пусть О – центр вписанной окружности в осевом сечении конуса. По условию РAOC = a, тогда РAOD = 180° - a. Очевидно, что a > 90°. Из прямоугольного треугольника AOD находим РOAD =  180° - (90° + 180° -a) = a - 90°. АО – биссектриса РCAD. Следовательно, РCAD = 2РOAD = 2 a - 180°.  OD =R. Тогда из треугольника AOD находим AD.  AD = OD tg AOD = R tg(180° -a) = -R tga.

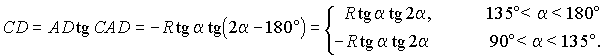
      Подставив найденные величины в формулу объема, получим

.

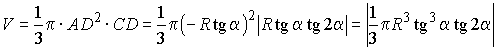      Если 90° < a < 135°, то 180° < 2a < 270°; тогда tg a< 0, tg 2a >0 и

.

      Если 135° < a < 180°, то 270° < a < 360°; тогда tg 2a < 0, tg 2a < 0 и

.

      Ответ: 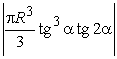.