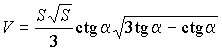7.8.1. 1972 г. У боковой грани правильной треугольной пирамиды площадь равна S и угол при основании равен a. Найти объем пирамиды. При каком условии задача имеет решение?

      Ответ: 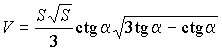, 30° <  a< 90° .

      7.8.2. 1973 г. В правильной треугольной пирамиде дан двугранный угол a между основанием и боковой гранью. Найти угол между боковыми гранями.

      Ответ: .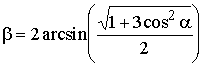

      7.8.3. 1973 г. Из точки ребра двугранного угла 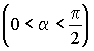 исходят два луча, расположенные в различных полуплоскостях его. Один из этих лучей перпендикулярен ребру, а другой образует острый угол b с ребром. Найти угол между данными лучами.

      Ответ: cos w = sin a Ч sin b.

      7.8.4. 1974 г. Сторона основания правильной четырехугольной пирамиды равна a, плоский угол при вершине пирамиды равен a. Найти расстояние от центра основания пирамиды до ее бокового ребра.

      Ответ: .

      7.8.5. 1975 г. В правильной четырехугольной пирамиде двугранные углы при основании равны a. Найти объем пирамиды, если ее полная поверхность равна P.

      Ответ: .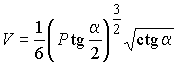

      7.8.6. 1975 г. Основанием прямой призмы служит прямоугольный треугольник с гипотенузой c и острым углом a. Через гипотенузу нижнего основания и вершину прямого угла верхнего основания проведена плоскость, образующая с плоскостью основания угол b. Определить объем треугольной пирамиды, отсеченной от призмы плоскостью.

      Ответ: .

      7.8.7. 1980 г. Сторона основания правильной треугольной призмы меньше бокового ребра и равна a. Через сторону верхнего основания проведена плоскость, которая с плоскостью основания составляет угол 45°  и делит призму на две части. Определить объем верхней части призмы.

      Ответ: .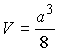

      7.8.8. 1980 г. Основанием прямой призмы служит прямоугольный треугольник с гипотенузой, равной c, и углом 30°. Через гипотенузу нижнего основания и вершину прямого угла верхнего основания проведена плоскость, образующая с плоскостью основания угол 45°. Определить объем треугольной пирамиды, отсеченной от призмы плоскостью.

      Ответ: .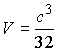

      7.8.9. 1990 г. Плоские углы трехгранного угла равны 45°,45° и 60°. Через его вершину проведена прямая, перпендикулярная к одной из граней, плоский угол которой равен O. Найти угол между этой прямой и ребром трехгранного угла, не лежащим в упомянутой грани.

      Ответ: 45°.

      7.8.10. 1992 г. Основанием прямой призмы служит равнобедренный треугольник с основанием a и противолежащим углом 2a Ј 60°. Через основание треугольника проведена плоскость, составляющая с плоскостью основания призмы угол 60°. Найти площадь сечения, если высота призмы равна a.

      Ответ: .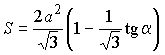

      7.8.11. 1993 г. В правильной четырехугольной пирамиде ABCDS боковые ребра равны l, а угол при основании боковой грани равен b. Через вершины A, B и точку  на ребре DS проведена секущая плоскость так, что . Определить вид и периметр полученного сечения.

      Ответ:  – равнобокая трапеция; периметр .

      7.8.12. 1993 г. В правильной четырехугольной пирамиде ABCDS сторона основания a и угол при вершине боковой грани равен a. На ребре DS выбрана точка  так, что . Через вершины A, B и точку  проведена секущая плоскость. Определить вид и периметр полученного сечения.

      7.8.13. 1993 г. Правильный тетраэдр с ребром 3 рассечен плоскостью так, что сечением является непрямоугольный четырехугольник, а вершины его делят ребра тетраэдра на отрезки длины 1 и 2. Установить вид сечения и найти его площадь.

      Ответ: равнобедренная трапеция с площадью  ед.

      7.8.14. 1973 г. Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда наклонены к плоскости основания под углами a и b. Найти угол между этими диагоналями.

      Ответ: cos w = sin a sin b.

      7.8.15. 1973 г. В основании пирамиды лежит правильный треугольник, а ее боковые ребра имеют длину 1. Найти плоский угол при вершине пирамиды, если ее объем равен .

      Ответ: .