@Тело, полученное при вращении полукруга вокруг диаметра, называется шаром, а поверхность, образуемая при этом вращении, называется шаровой поверхностью или сферой.

      Всякое сечение шара плоскостью есть круг. Если плоскость проходит через центр шара, то сечение называется большим кругом (радиус этого круга равен радиусу шара).

      Часть шаровой поверхности, отсекаемая от нее какой-нибудь плоскостью, называется сегментной поверхностью.

      Часть шаровой поверхности, заключенная между двумя параллельными секущими плоскостями, называется шаровым поясом.

      Параметрами, связанными с шаром, являются: радиус (R), площадь большого круга (), площадь поверхности шара (), объем V.

      Любой из этих параметров определяет шар.

     К формулам, связывающим параметры шара, относятся

, , .

      Сегментная поверхность (поверхность шарового пояса) равна длине окружности большого круга на высоту сегментной поверхности (поверхности шарового пояса) S = 2pRH.
 

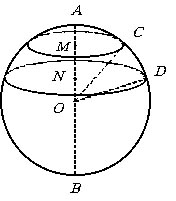Тело, полученное от вращения кругового сектора COD (AOC) вокруг диаметра АВ, не пересекающего, ограничивающую его дугу, называется шаровым сектором.  АМ – высота сегментной поверхности, образованной вращением сектора АОС.  MN – высота шарового пояса, образованного вращением сектора COD.

      Объем шарового сектора равен произведению поверхности соответствующего шарового пояса (или соответствующей сегментной поверхности) на треть радиуса

V _сект , V _сегм .

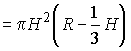      Поверхности шаров относятся как квадраты их радиусов, объемы шаров относятся как кубы радиусов.

Упражнение 7.5.1.

      1. Дано:  (большого круга). Найти R, , V.

      2. Дано: V. Найти R, .

      Ответ: 1. , , ; 2. , .

Пример 7.5.2.

      На поверхности шара даны три точки. Прямолинейные расстояния между ними 6 см, 8 см, 10 см. Радиус шара 13 см. Найти расстояние от центра шара до плоскости, проходящей через эти три точки.

Соединив эти точки между собой и центром шара О, легко заметить, что задача свелась к нахождению высоты (OD) треугольной пирамиды OABC. Основание высоты (D) должно совпадать с центром окружности, описанной около треугольника АВС. Стороны АВ, АС и ВС, равные прямолинейным расстояниям между точками А, В, С, удовлетворяют теореме Пифагора , т.е. треугольник АВС – прямоугольный, и точка D является серединой гипотенузы АВ. Тогда из прямоугольного треугольника BOD находим OD   ,OD = 12 (см).

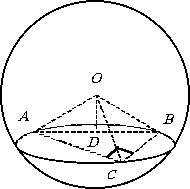
Пример 7.5.3.

     Радиус шара 15 м. Вне шара дана точка А на расстоянии 10 м от его поверхности. Найти длину такой окружности на поверхности шара, все точки которой отстоят от точки А на 20 м.

Искомая окружность является окружностью основания конуса, образующие которого равны расстоянию от точки А до этой окружности, т.е. 20 м. Тогда в плоскости, проходящей через центр шара О и точку А рассмотрим треугольник АВО, где В – точка искомой окружности.  По условию AD = 10 м, OD = OB = 15 м.  Тогда AO = AD + DO, AO = 25 м, AB = 20 м.

Стороны треугольника АВО удовлетворяют теореме Пифагора , следовательно, DABO – прямоугольный.  – высота, проведенная из вершины прямого угла В.Тогда из метрических соотношений в DABO имеем

     Откуда 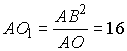 (м).

     Из прямоугольного треугольника  имеем

,  (м).

– радиус искомой окружности, тогда длина этой окружности .

     Ответ: 24 p.

Пример 7.5.4.

     Стороны треугольника 13 см, 14 см, 15 см. Найти расстояние от плоскости треугольника до центра шара, касательного к сторонам треугольника. Радиус шара 5 см.

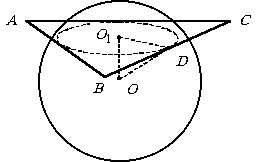Плоскость треугольника АВС пересекает поверхность шара по окружности, вписанной в треугольник АВС. Искомое расстояние – это расстояние между центром этой окружности 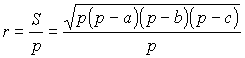 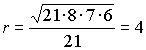и центром шара О. Найдем радиус этой окружности  по формуле   , где  (см),  (см).

      Треугольник  – прямоугольный, так как  перпендикулярно плоскости треугольника АВС, следовательно и любой прямой, лежащей в этой плоскости. Тогда , где OD – радиус шара.  (см).

     Ответ: 3 см.

Пример 7.5.5.

     Полукруг радиуса R, разделенный двумя радиусами на три равные части, вращается вокруг диаметра. Найти объемы тел, полученных от вращения каждой части.

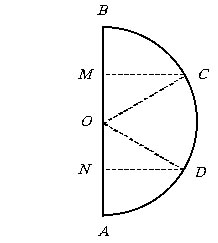По условию части ОВС, OCD и OAD равны, следовательно, центральные углы РBOC, РCOD и РDOA равны и составляют 60°. Из прямоугольного треугольника OMC находим ОМ  , тогда .        Аналогично , MN = R.  BM и AN – высоты равных шаровых сегментов.

V _сект ,

V _сект .

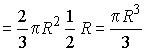      Объем шарового сектора OCD найдем как разность между объемом шара и объемами найденных секторов ОВС и AOD

.

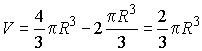      Ответ: , .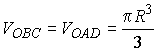

Пример 7.5.6.

      Шар образован вращением полукруга вокруг прямой, содержащей диаметр. При этом поверхность, образованная вращением некоторой хорды, один конец которой совпадает с концом данного диаметра, разбивает шар на две равные по объему части. Найти косинус угла между этой хордой и диаметром.

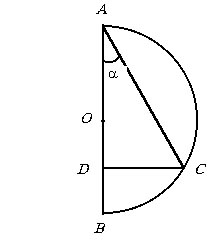Объем одной из частей состоит из объема конуса и объема шарового сегмента. Пусть AC = a, AB = 2R и РCAB = a.  Тогда из прямоугольного треугольника АВС находим a = 2R cos a. Из прямоугольного треугольника ACD находим AD и DC   , DC = a sin a = R sin 2a.  Тогда . AD – высота конуса, BD – высота шарового сегмента, DC – радиус основания конуса.

V _кон ,

V _сегм .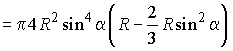

Согласно условию задачи V _кон + V _сегм V _{ш, т.е.}

,

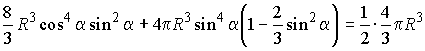откуда .

      После преобразования имеем

, ,

откуда , .

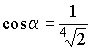      Ответ: .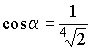

Пример 7.5.7. (КубГУ, физич., 1979 г.)

      Шар радиуса r освещается точечным источником света. Его тень на стене представляет собой круг радиуса R. Найти расстояние источника света от поверхности шара, если освещенная часть вдвое меньше тени.

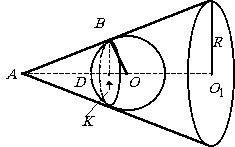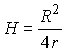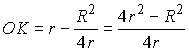Освещенная часть шара представляет собой сегментную поверхность S сегм = 2 prH, где H = KD. По условию задачи , откуда .

OK = OD - KD, .

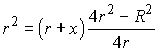      Пусть AD = x, тогда из метрических соотношений в прямоугольном треугольнике ABD имеем  или , откуда .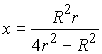

     Ответ: 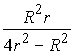.