@Конической поверхностью называется поверхность, образованная вращением прямой, пересекающей некоторую неподвижную прямую (ось вращения) вокруг этой оси. Точка пересечения называется вершиной конической поверхности.
Прямым круговым конусом (в дальнейшем просто конусом) называется тело, ограниченное конической поверхностью, расположенной по одну сторону от вершины, и плоскостью, перпендикулярной оси вращения (основание конуса).
Часть конической поверхности, от вершины до основания, называется боковой поверхностью конуса, часть образующей от вершины до основания называется образующей конуса. В основании конуса лежит круг.
Сечение конуса плоскостью, проходящей через ось конуса (осевое сечение), есть равнобедренный треугольник, высота которого совпадает с высотой конуса, а основание равно диаметру основания конуса.
Любое сечение конуса, проходящее через вершину, есть равнобедренный треугольник, боковые стороны которого равны образующим конуса.
Сечением конуса, пересекающим только его боковую поверхность, является часть плоскости, ограниченной эллипсом или окружностью, если сечение перпендикулярно оси конуса.
Если боковую поверхность конуса разрезать вдоль образующей, то получится круговой сектор, который называется разверткой боковой поверхности конуса. Радиус этого сектора равен образующей конуса, а длина дуги равна длине окружности основания.
Параметрами, связанными с
конусом, являются: радиус основания (R), высота (Н), образующая (L), площадь
основания (
),
площадь осевого сечения ( 
), площадь боковой поверхности (
),
площадь полной поверхности (
),
объем конуса (V), угол наклона образующей к плоскости основания (a),
угол при вершине осевого сечения конуса (b).
Очевидно, R и ;
a
и b
являются зависимыми параметрами.
Любых два независимых параметра определяют конус.
К формулам, связывающим параметры конуса, относятся:
, 
, 
, 
.Полезно, применяя эти формулы, по двум независимым параметрам уметь находить остальные.
Упражнение 7.4.1.
1. Дано: R и a.
Найти: H, L, , , ,
V.
2. Дано: и L.
Найти: H, R, , ,
V.
3. Дано: H и V. Найти:
R, L, , , ..
4.
Дано: и
b . Найти: R, H, L, ,
V.
5. Дано: и V.
Найти: R, H, L, , .
Ответ: 1.R tg a, 
, 
, 
, 
, 
.
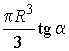2. 
, 
, 
, 
, 
.
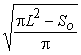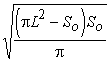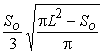3. 
, 
, 
, 
, 
.
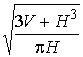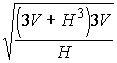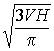4. 
, 
, 
, 
, 
.
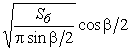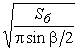5. 
, 
, 
, 
, 
.
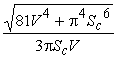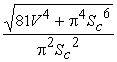Пример 7.4.2. (КубГУ, матем., 1979 г.)
Через вершину конуса проведена плоскость под углом a к основанию. Эта плоскость пересекает основание по хорде АВ длины a, стягивающей дугу основания конуса, которой соответствует центральный угол величины b . Найти объем конуса.
 |
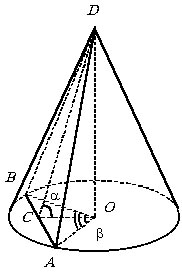Угол a –
это угол между высотой равнобедренного треугольника ADB,
полученного в сечении, и ее проекцией на основание конуса. РDCO
= a.
Из прямоугольного треугольника АСО найдем АО и ОС
Из прямоугольного треугольника OCD найдем OD OD = H OC tg a,
т.е |
.
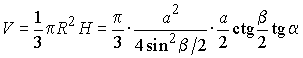
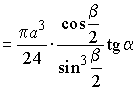Ответ: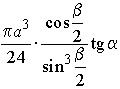 
.
Пример 7.4.3. (КубГУ, физич., 1973 г.)
Боковая поверхность конуса вдвое больше площади основания. Найти угол его развертки.
По условию S бок
= 2S осн,
т.е 
,
откуда 
.
С другой стороны площадь развертки – это площадь кругового сектора радиуса
L с искомым центральным углом
a.
, 
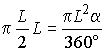,откуда 
.
Ответ: развертка – полукруг, a = p.
Пример 7.4.4. (КубГУ, физич., 1979 г.)
Разность между образующей конуса и его высотой равна d , а угол между ними равен a. Найти объем конуса.
Из условия следует, что L = H + d и
H = L cos a.
Тогда 
, откуда 
.
Из этого же треугольника имеем R = H tg a,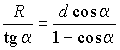 
,
т.е. 
.
Тогда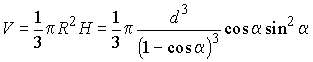 
.
Ответ: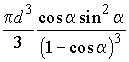 
.
@ Усеченным конусом называется часть полного конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.
Осевое сечение усеченного конуса – равнобедренная трапеция, основания которой равны диаметрам оснований конуса, а боковые ребра – образующие конуса.
Если обозначить радиусы оснований конуса r и R, то имеют место формулы
,
, 
.Пример 7.4.5.
Площадь осевого сечения усеченного конуса равна разности площадей оснований, а радиусы оснований равны R и r. Определить объем усеченного конуса.
Из условия имеет место соотношение 
,
откуда H = p(R -
r). Тогда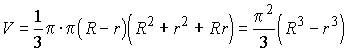 
.
Ответ: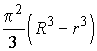 
.
, 
.
.