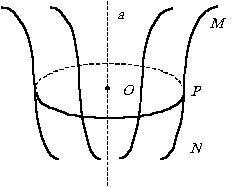
Если через произвольную точку Р поверхности вращения провести плоскость, перпендикулярную оси вращения, то в сечении получится круг, линия пересечения поверхности вращения с секущей плоскостью – окружность, центр которой находится в точке пересечения секущей плоскости с осью вращения.

@Цилиндрической поверхностью называется поверхность, образованная вращением прямой, параллельной оси вращения.

     Прямым круговым цилиндром называется тело, ограниченное цилиндрической поверхностью и двумя плоскостями, перпендикулярными оси цилиндра. В дальнейшем такое тело будем называть просто цилиндром.

     Часть поверхности между этими плоскостями называется боковой поверхностью цилиндра, круги, полученные в секущих плоскостях – основаниями цилиндра, часть образующей между основаниями называется образующей цилиндра.

     Сечение, проходящее через ось цилиндра – осевое сечение, есть прямоугольник со сторонами, равными высоте цилиндра и диаметру основания.

     Сечение, параллельное оси цилиндра – прямоугольник, стороны которого равны высоте цилиндра и хорде основания, не проходящей через центр.

     Сечение, не перпендикулярное оси цилиндра, пересекающее боковую поверхность и не пересекающее основания цилиндра, представляет часть плоскости, ограниченную эллипсом.

     Если боковую поверхность цилиндра разрезать вдоль образующей и развернуть, то получится прямоугольник, называемый разверткой боковой поверхности цилиндра, стороны которого равны высоте цилиндра и длине окружности основания.

     Основные параметры, связанные с цилиндром: радиус основания (R), высота (Н), образующая (L), площадь основания (), площадь осевого сечения (), площадь боковой поверхности (), площадь полной поверхности (), объем цилиндра (V).

     Любые пары перечисленных параметров кроме пар: высота и образующая, радиус основания и площадь основания, площадь осевого сечения и площадь боковой поверхности задают цилиндр, т.е. определяют его однозначно.

    К формулам, связывающим эти понятия, относятся

 ; ; ;

 ; .

      Полезно по паре заданных параметров с помощью приведенных формул находить остальные.

Упражнение 7.3.1.

      1. Дано: R и H. Найти: , , , V.

      2. Дано: R и . Найти: H, , , V.

      3. Дано:  и V. Найти: R, H, , .

      4. Дано: H и V. Найти: R, , , .

      Ответ: 1. , 2 pRH, 2 p(R + H), .

                 2. , , , .

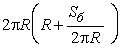                 3. ,  , , .

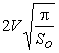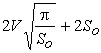                 4. , , , .

       Многие задачи, связанные с телами вращения, очевидным образом и сразу сводятся к задачам планиметрии.

Пример 7.3.2.

      Высота цилиндра Н, радиус основания R. Сечение плоскостью, параллельной оси цилиндра, – квадрат. Найти расстояние этого сечения от оси.

Из условия следует, что , тогда , OA = R. Из прямоугольного треугольника АСО имеем   , .  Ответ: .

      Осевое сечение цилиндра – квадрат, площадь которого равна Q. Найти площадь основания.

      Так как сторона данного квадрата равна диаметру основания, то . Тогда S

_осн .

      Ответ: .

Пример 7.3.4.

      Площадь осевого сечения цилиндра равна Q. Найти площадь боковой поверхности.

       Из определения осевого сечения следует, что его стороны равны Н и 2R. Тогда Q = 2 RH, S _бок = 2 pRH = pQ.

      Ответ: pQ.

Пример 7.3.5.

       Боковая поверхность и объем цилиндра выражаются одним числом. Определить диаметр цилиндра.

     По условию , откуда R = 2. Тогда 2R = 4.

     Ответ: 4 лин. ед.

Пример 7.3.6.

      Высота цилиндра равна Н и в развертке его боковой поверхности образующая составляет с диагональю угол 60°. Определить объем цилиндра.

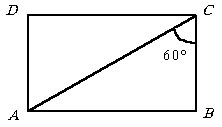Развертка – прямоугольник ABCD – со сторонами, равными высоте цилиндра и длине окружности основания. BC = H, AB = 2 pR. Тогда из прямоугольного треугольника ABC находим BC = ABctg60°. Откуда  и .

      Подставив в формулу объема, получим .

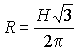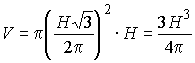      Ответ: .

Пример 7.3.7.

      Вершины А и В прямоугольника ABCD лежат на окружности одного из оснований цилиндра, а С и D – на окружности другого основания. Вычислить радиус цилиндра, если его образующая равна a, AB = a, а угол между прямой ВС и плоскостью основания равен 60°.

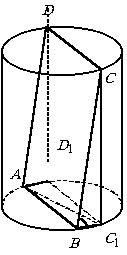Угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость, следовательно, , , тогда из прямоугольного треугольника  находим  .  Так как  и DC = AB, то четырехугольник  – прямоугольник со сторонами a и , диагональ которого равна диаметру основания.

      Откуда следует, что , , .

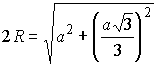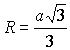      Ответ: .