Для любой пирамиды справедливы равенства
|
|
(8)
|
|
|
(9)
|
S бок – площадь боковой поверхности (сумма площадей боковых граней);
S осн – площадь основания пирамиды;
V – объем пирамиды;
h – высота пирамиды.
Для правильной пирамиды также имеем
S бок
= ![]() P
осн Ч 1
(10)
P
осн Ч 1
(10)
где P осн – периметр основания пирамиды;
1 – длина апофемы (высоты боковой грани, опущенной из вершины пирамиды).
Часть пирамиды, заключенная между плоскостью основания и плоскостью, проведенной параллельно основанию с пересечением боковых ребер пирамиды, называют усеченной пирамидой. Основание пирамиды и сечение указанной плоскостью исходной пирамиды называют основаниями усеченной пирамиды. Остальные грани усеченной пирамиды называют боковыми. Ребра, не принадлежащие основаниям, называют боковыми ребрами. Расстояние между плоскостями оснований называют высотой усеченной пирамиды, часто высотой усеченной пирамиды также называют любой отрезок, перпендикулярный плоскостям оснований и имеющий концы на этих плоскостях. Ясно, что основания усеченной пирамиды подобны. Если ее основания – правильные многоугольники и все ее боковые ребра равны, то такую усеченную пирамиду называют правильной.
Для произвольной усеченной пирамиды имеют место равенства
|
|
(11)
|
|
|
(12)
|
S бок – площадь боковой поверхности (сумма площадей боковых граней – трапеций);
![]() ,
, ![]() – площади оснований;
– площади оснований;
V – объем усеченной пирамиды.
h – высота усеченной пирамиды;
Для правильной усеченной пирамиды также имеем
S бок
= ![]() , (13)
, (13)
где ![]() ,
, ![]() – периметры оснований;
– периметры оснований;
1 – апофема (высота боковой грани – трапеции).
Упражнение 7.2.1.
Показать, что для любой пирамиды (усеченной пирамиды) справедлива формула Эйлера.
Указание. Желательно определить числа вершин, ребер и граней в n-угольной пирамиде (усеченной пирамиде).
При решении задач, связанных с пирамидой, полезными являются приведенные далее утверждения 1 – 3.
Утверждение 1.
Следующие три предложения а) – в) равносильны:
а) ортогональная проекция вершины пирамиды на плоскость основания является центром описанной окружности около многоугольника в основании;
б) боковые ребра пирамиды равны;
в) боковые ребра образуют равные (острые) углы с плоскостью основания пирамиды.
Утверждение 2.
Следующие три предложения а) – в) равносильны:
а) ортогональная проекция вершины пирамиды на плоскость основания является центром вписанной окружности в многоугольник, лежащий в основании;
б) высоты боковых граней - треугольников, проведенные из вершины пирамиды, равны и лежат на соответствующих боковых гранях;
в) двугранные углы при основании пирамиды равны.
Утверждение 3.
Следующие три предложения а) – в) равносильны:
а) ортогональная проекция вершины пирамиды на плоскость основания равноудалена от прямых, содержащих стороны основания пирамиды;
б) высоты боковых граней - треугольников, проведенные из вершины пирамиды, равны;
в) плоскости боковых граней образуют равные углы с плоскостью основания.
Упражнение 7.2.2.
Доказать утверждения 1 – 3.
Указание. Рассматриваем n - угольную пирамиду ![]() ,
у которой О – ортогональная проекция вершины S
на плоскость основания
,
у которой О – ортогональная проекция вершины S
на плоскость основания ![]() ,
а
,
а ![]() – основания
высот боковых граней -треугольников соответственно
– основания
высот боковых граней -треугольников соответственно ![]() ,
, ![]() ,
...
,
... ![]() ,
проведенных из вершины S.
,
проведенных из вершины S.
Каждое из предложений а) – в) в утверждении 1 обеспечивает равенство треугольников ![]() ,
, ![]() ,
...
,
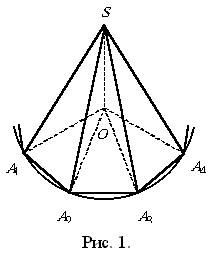
... ![]() (рис. 1), откуда легко получаем доказательство этого утверждения.
(рис. 1), откуда легко получаем доказательство этого утверждения.
|
Построим треугольники |
|
Пример 7.2.3.
В основании пирамиды лежит равносторонний треугольник со стороной a. Найти объем пирамиды, если известно, что плоскости боковых граней наклонены к плоскости основания под углом 60° .
|
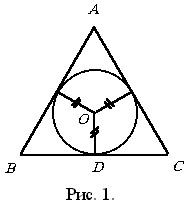
Пусть SABC – данная пирамида, О – ортогональная проекция
вершины S на плоскость основания
АВС. Согласно утверждению 3, точка О равноудалена от прямых
АВ, ВС и АС. Не ограничивая
общности рассуждений, имеем два случая расположения точки О: а) О находится
внутри треугольника АВС, т.е. является центром вписанной окружности (рис.
1); б) О находится вне треугольника АВС, т.е. является центром вневписанной
окружности (рис. 2). Полагая, что D –
точка пересечения прямых АО и ВС (ясно, что D
– точка касания окружности с ВС), в случае а) имеем 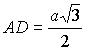 получаем получаем 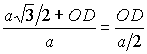 и
и 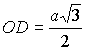 . .
Из прямоугольного треугольника SOD ввиду РSDO = 60° (рис 3 и 4) находим Откуда в случаях а) и б) соответственно имеем |
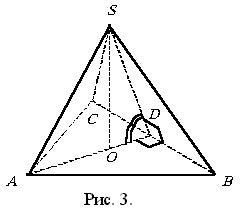
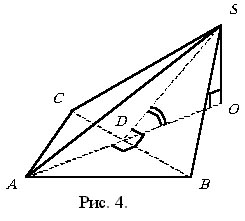
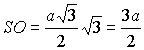 ,
а значит, в силу
,
а значит, в силу 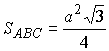 окончательно по формуле (9) получаем
окончательно по формуле (9) получаем
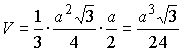 в случае а)
в случае а)
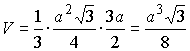 в случае б).
в случае б).
Ответ: ![]() или
или ![]() .
.
Упражнение 7.2.4. (КубГУ, матем., 1982 г.)
В основании треугольной пирамиды лежит треугольник с острыми углами a и b. Боковые ребра наклонены к плоскости основания под углом f , высота пирамиды равна H. Найти объем.
Указание. Можно использовать утверждение 1.
Ответ: ![]() .
.
Для тренировки рекомендуем самостоятельно выполнить следующие упражнения 7.2.5 и 7.2.6.
Упражнение 7.2.5.
Элементами пирамиды будем называть длины сторон оснований и боковых ребер, высоту, площади основания, боковой и полной поверхностей, объем, плоские углы при вершине (углы между боковыми ребрами, принадлежащими одной грани) и плоские углы при основании (углы между сторонами оснований и боковыми ребрами), двугранные углы между смежными боковыми гранями и между основанием и боковыми гранями. Для правильной n - угольной пирамиды сформулировать и решить несколько задач, в которых по известным двум элементам можно определить все другие элементы.
Указание. Примером одной из таких задач может быть следующая: сторона основания правильной n - угольной пирамиды равна a и площадь боковой поверхности равна S. Найти боковое ребро, высоту, площадь основания, площадь полной поверхности, объем, плоские углы на всех гранях и двугранные углы между любыми двумя смежными гранями.
Заметим, что таких задач можно сформулировать более сорока.
Упражнение 7.2.6.
Элементами усеченной пирамиды будем называть длины сторон двух ее оснований и боковых ребер, высоту, площади оснований, боковой и полной поверхностей, объем, плоские углы на гранях и двугранные углы между смежными гранями. Для правильной n - угольной усеченной пирамиды сформулировать и решить несколько задач, в которых по трем известным элементам можно определить все другие элементы.
Определенный интерес представляют задачи на правильную пирамиду, в которых по одному известному элементу можно найти другой элемент.
Пример 7.2.7. (КубГУ, матем., 1973 г.)
В правильной треугольной пирамиде дан двугранный угол a между основанием и боковой гранью. Найти угол между боковыми гранями.
 |
Пусть D – середина ребра ВС
в правильной пирамиде SABC (см.
рисунок). Так как DBSC
и DBAC
равнобедренные, то AD и SD
перпендикулярны ВС, а значит по условию РADS
= a.
Теперь пусть Е – основание высоты из вершины В в DASB.
Так как DASB
= DASC,
то Е – основание высоты из вершины С в DASC,
т.е. РBEC
– искомый угол, который для краткости обозначим через b.
Ортогональная проекция О вершины
S на плоскость АВС попа-
дает в центр вписанной окружности в DABC и лежит на высоте AD. Полагая AB = BC = AC = a для радиуса вписанной окружности в DABC, имеем 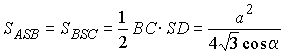 . . |
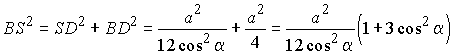 ,
откуда
,
откуда 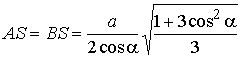 .
Из DBSD
получаем
.
Из DBSD
получаем
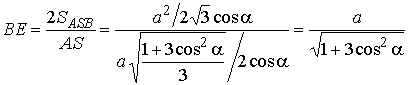 .
.
В равных треугольниках ASB и
ASC высоты BE
и CE тоже равны, поэтому
DBEC
равнобедренный и его медиана DE
является биссектрисой, т.е. ![]() .
Из прямоугольного треугольника BED
находим
.
Из прямоугольного треугольника BED
находим ![]() ,
т.е.
,
т.е. 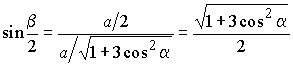 .
Поэтому окончательно получаем
.
Поэтому окончательно получаем 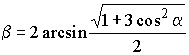 .
.
Ответ: 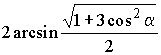 .
.
Замечание. В правильной усеченной пирамиде
тоже иногда можно по одному известному элементу найти другой элемент. Например,
если бы в правильной усеченной пирамиде угол между основанием и боковой
гранью был равен a
(несущественно a
– тупой или нет), то, достроив ее до правильной треугольной пирамиды, по
аналогии с решением примера 7.2.7 мы бы нашли угол между смежными боковыми
гранями, который будет равен 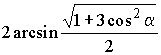 .
.
Упражнение 7.2.8.
В правильной усеченной четырехугольной
пирамиде боковое ребро равно 5, а двугранный угол при большем основании
равен arccos 0,75. Найти сторону меньшего основания этой пирамиды,
если ее объем равен ![]() .
.
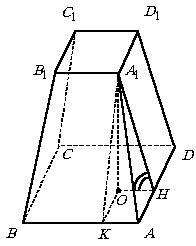 |
Указание. О – ортогональная
проекция вершины
|
Ответ: 10.
Теперь рассмотрим некоторые задачи, когда пирамида (усеченная пирамида) не является правильной.
Пример 7.2.9. (КубГУ, эконом., 1992 г.)
Основанием пирамиды служит прямоугольный треугольник, один из острых углов которого равен a. Каждое боковое ребро наклонено к плоскости основания под углом b. Найти длину бокового ребра, если объем пирамиды равен V.
 |
Согласно утверждению 1, ортогональная проекция О вершины S
пирамиды SABC попадает в центр
описанной около треугольника АВС окружности. Так как DABC
прямоугольный, то О – середина гипотенузы (см. рисунок). Для краткости
полагаем SO = h и AC = c. Из прямоугольного треугольника
АВС ввиду того, что РBAC
= a,
находим AB = c cos a
и BC = c sin a.
Откуда
|
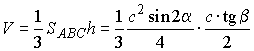 или
или 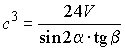 ,
т.е.
,
т.е. 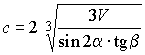 .
.
Откуда из DAOS окончательно находим
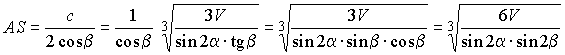 .
.
Ответ: 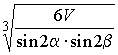 .
.
Упражнение 7.2.10. (КубГУ, эконом., 1989 г.)
Основанием пирамиды служит правильный треугольник АВС, длина стороны
которого ![]() .
Основанием высоты, опущенной из вершины S,
является точка О, лежащая внутри треугольника АВС. Расстояния
от точки О до сторон АВ, ВС
и СА находятся в отношении 2 : 1 : 3 соответственно. Площадь
грани SBC равна
.
Основанием высоты, опущенной из вершины S,
является точка О, лежащая внутри треугольника АВС. Расстояния
от точки О до сторон АВ, ВС
и СА находятся в отношении 2 : 1 : 3 соответственно. Площадь
грани SBC равна ![]() .
Найти длину высоты пирамиды.
.
Найти длину высоты пирамиды.
Указание. Высоты треугольников АОВ, ВОС
и АОС соответственно равны 2k, k
и 3k, а сумма их площадей равна ![]() .
Откуда можно найти k, т.е. расстояние
от О до ВС.
.
Откуда можно найти k, т.е. расстояние
от О до ВС.
Ответ: 1,5.
Пример 7.2.11.
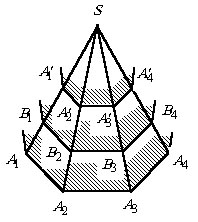
Площади верхнего и нижнего оснований усеченной пирамиды соответственно равны 1 и 4 (кв. ед). Параллельно основанию проведена плоскость, делящая пирамиду на две равновеликие части. Определить площадь сечения и отношение, в котором секущая плоскость делит высоту пирамиды.
Сначала отметим, что отношение
объемов подобных тел равно кубу коэффициента подобия. Для применения этого
факта достроим данную усеченную пирамиду ![]() до пирамиды
до пирамиды ![]() (см. рисунок).
(см. рисунок).
Полагаем, что объем пирамиды ![]() равен
равен ![]() и
и ![]() – многоугольник
с искомой площадью S, являющейся
сечением, разбивающим данную усеченную пирамиду на две равновеликие части
с объемами
– многоугольник
с искомой площадью S, являющейся
сечением, разбивающим данную усеченную пирамиду на две равновеликие части
с объемами ![]() .
.
Пирамиды ![]() ,
, ![]() и
и ![]() подобны
(гомотетичны с центром S), причем
коэффициент подобия первой и второй равен
подобны
(гомотетичны с центром S), причем
коэффициент подобия первой и второй равен ![]() ,
а первой и третьей –
,
а первой и третьей – ![]() (учли, что отношение площадей подобных фигур равно квадрату их коэффициента
подобия).
(учли, что отношение площадей подобных фигур равно квадрату их коэффициента
подобия).
 |
Откуда следует, что объем данной усеченной пирамиды равен |
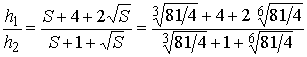 ,
,после некоторых преобразований
получаем 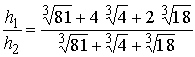 .
.
Ответ: ![]() (кв. ед.) и
(кв. ед.) и ![]() .
.
Упражнение 7.2.12.
Доказать, что если плоскость, параллельная основаниям усеченной пирамиды, делит эту пирамиду на две равновеликие части, то площадь сечения равна
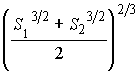 ,
,где ![]() и
и ![]() – площади
оснований данной пирамиды.
– площади
оснований данной пирамиды.
Указание. Рассуждения при доказательстве подобны рассуждениям в примере 7.2.11 при нахождении площади сечения S.
Рассмотрим довольно часто
встречающуюся на вступительных экзаменах ситуацию.
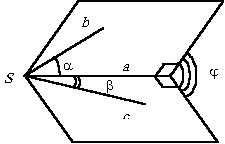 |
Пусть a – ребро двугранного угла, равного f, S – точка на a, b и c – лучи, лежащие на сторонах двугранного угла с началом в точке S такие, что острые углы, образованные лучами b и c с прямой a, соответственно равны a и b (см. рисунок). Чему равен угол между лучами b и c? |
Пример 7.2.13.
В треугольной пирамиде SABC ребро SA перпендикулярно плоскости основания АВС, причем РASB = a, РASC = b, РBAC = f. Найти угол BSC.
Сначала отметим, что если в ситуации, приведенной до примера 7.2.13, провести плоскость, перпендикулярную к прямой a, то поставленный вопрос соответствует условию этого примера и в этом случае искомый угол между лучами b и c будет равен углу BSC (покажите это подробнее!).
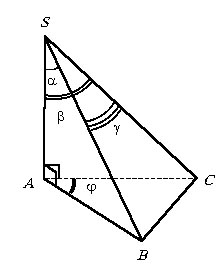 |
Для удобства положим, что РBSC
= g
и SA = x. Из прямоугольного DASB
получаем AB = x tg a
и 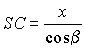 . По теореме косинусов
в DBAC
находим . По теореме косинусов
в DBAC
находим |
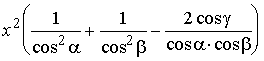 .
.
Откуда, приравнивая правые части полученных равенств для ![]() ,
после некоторых преобразований получим:
,
после некоторых преобразований получим:
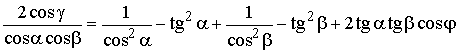 ,
,т.е. 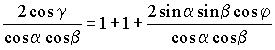 и окончательно cosg
= cosa
cosb
+ sina
sinb
cosf.
и окончательно cosg
= cosa
cosb
+ sina
sinb
cosf.
Ответ: arccos(cosa cosb + sina sinb cosf).
Замечание. Равенство, полученное в примере 7.2.13
называют аналогом теоремы косинусов для трехгранного угла (с вершиной S и ребрами SA, SB, SC). Это равенство (14) полезно запомнить. Оно дает возможность по трем известным углам из a, b, g и f, где a, b О(o;p/2) и g, f О(o;p), определить оставшийся четвертый угол. Оказывается в некоторых ситуациях можно даже по двум известным углам из указанных определить два других. Одна из таких известных в школьном курсе ситуаций описана в следующем задании.
Упражнение 7.2.14.
В пирамиде OABC ребро ОB
перпендикулярно основанию АВС, а ребро АС перпендикулярно
грани ВОС, причем РBOC
= g
и РABC
= f.
Найти углы ВОА и АОС.
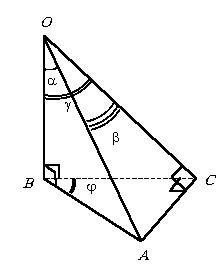 |
Указание. Обозначим РBOA
= a
и РAOC
= b;
ясно, что все углы a,
b, g
и f – острые
(см. рисунок). Дальнейшее решение полностью соответствует решению задачи
2 в § 19 п. 167 учебника А.В.Погорелова “Геометрия 7 – 11” (М.; 1993).
Ответ: РBOA = arctg (tgg / cos f) |
Пример 7.2.15. (КубГУ, матем., 1993 г.)
Правильный тетраэдр с ребром 3 рассечен плоскостью так, что сечением является непрямоугольный четырехугольник, а вершины его делят ребра тетраэдра на отрезки длиной 1 и 2. Установить вид сечения и найти его площадь.
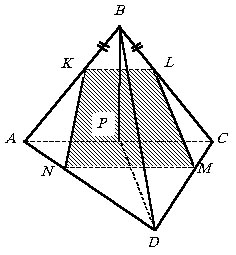 |
С точностью до обозначения буквами вершин тетраэдра можно считать, что вершины К, L, M и N сечения лежат на ребрах АВ, ВС, CD и AD соответственно. Сначала рассмотрим ситуацию, когда BK = BL (см. рисунок). В этой ситуации KL ||AC, а значит, прямая KL параллельна плоскости треугольника ADC. Поэтому плоскость, проходящая через KL, пересекает плоскость треугольника ADC по прямой, параллельной KL, т.е. KL ||MN. Откуда MN || AC, а значит, DN = DM. |
Не ограничивая общности рассуждений, по условию задачи можем считать, что BK = BL = 1 и DN = DM = 2 (при BK = BL = 2 и DN = DM = 1 получаем симметричную фигуру относительно плоскости симметрии тетраэдра, проходящей через ребро АС).
Ввиду правильности треугольников KBL
и NDM получаем KL = 1
и NM = 2. Из DANK
по теореме косинусов находим ![]() .
Аналогично из DCML
получаем
.
Аналогично из DCML
получаем ![]() .
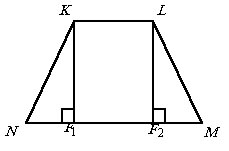
Итак, в этом случае сечение KLNM
является равнобедренной трапецией (см. рисунок). Пусть
.
Итак, в этом случае сечение KLNM
является равнобедренной трапецией (см. рисунок). Пусть ![]() и
и ![]() – основания перпендикуляров
из К и L на NM
соответственно. Из
– основания перпендикуляров
из К и L на NM
соответственно. Из ![]() имеем
имеем ![]() .
.
 |
Так как Откуда следует, что
|
Осталось показать, что другие случаи невозможны. Предположим противное,
т.е. любые две вершины сечения разноудалены от вершины тетраэдра, в которой
пересекаются ребра, содержащие эти две вершины. Не ограничивая общности
рассуждений, можно считать, что BK = CL = DM = AN = 1 (см. рисунок).
 |
Из равенства треугольников NAK, KBL, LCM и MDN следует NK = KL = LM = MN, т.е. KLMN – ромб, а значит, KN || LM. По признаку параллельности прямой и плоскости получаем, что прямая KN параллельна плоскости треугольника BCD. Так как AK = 2 и AN = 1, то , а значит, прямые NK и DB пересекутся в плоскости треугольника ABD, что противоречит параллельности прямой KN и плоскости треугольника BCD. Пришли к противоречию. |
Упражнение 7.2.16. (КубГУ, эконом., 1993 г.)
Вычислить площадь ортогональной проекции правильного тетраэдра с ребром a на плоскость, параллельную его двум скрещивающимся ребрам.
Указание. Показать, что ортогональная проекция представляет собой квадрат
со стороной ![]() .
.
Ответ: ![]() .
.
В заключение приведем некоторые задачи, в которых рассматриваются конфигурации из многогранников.
Пример 7.2.17. (КубГУ, матем., 1979 г.)
В правильную треугольную пирамиду SABC,
боковое ребро которой имеет длину 1 и наклонено к плоскости основания
под углом a,
вписана треугольная призма ![]() ,
верхнее основание которой совпадает с сечением пирамиды SABC
некоторой плоскостью, а нижнее лежит на основании пирамиды. При какой длине
ребра основания призмы призма имеет наибольший объем?
,
верхнее основание которой совпадает с сечением пирамиды SABC
некоторой плоскостью, а нижнее лежит на основании пирамиды. При какой длине
ребра основания призмы призма имеет наибольший объем?
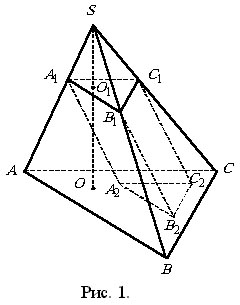
Пусть ![]() и О – ортогональные
проекции точки S на параллельные
плоскости
и О – ортогональные
проекции точки S на параллельные
плоскости ![]() и ABC
соответственно. Так как пирамида является правильной, то
и ABC
соответственно. Так как пирамида является правильной, то ![]() и ОС – радиусы описанных около равносторонних треугольников
и ОС – радиусы описанных около равносторонних треугольников ![]() и АВС окружностей. Ясно, что
и АВС окружностей. Ясно, что ![]() – расстояние между плоскостями
– расстояние между плоскостями ![]() и АВС ( что то же самое, между плоскостями
и АВС ( что то же самое, между плоскостями ![]() и
и ![]() (рис. 1).
(рис. 1).
 |
Заметим, что независимо от расположения основания призмы |
Далее, ![]() – коэффициент подобия D
– коэффициент подобия D![]() и DABC,
поэтому для радиусов описанных окружностей около этих треугольников имеем
и DABC,
поэтому для радиусов описанных окружностей около этих треугольников имеем ![]() ,
а значит, из подобия
,
а значит, из подобия ![]() и DSOC
(обоснуйте!) получаем
и DSOC
(обоснуйте!) получаем ![]() .
.
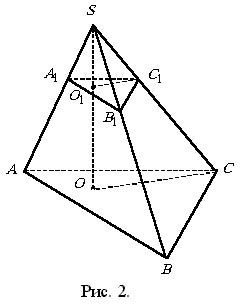 |
Учитывая, что (из DSOC)
SO = 1 sin a
и Откуда Замечая, что площадь верхнего
основания равна |
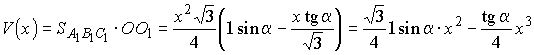 .
.
По смыслу задания xО(0;a),
т.е. ![]() .
Таким образом, задача свелась к нахождению значения x на промежутке
.
Таким образом, задача свелась к нахождению значения x на промежутке ![]() ,
при котором функция
,
при котором функция 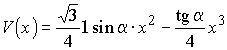 принимает наибольшее возможное значение.
принимает наибольшее возможное значение.
Имеем 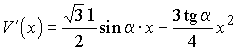 .
Так как коэффициент при
.
Так как коэффициент при ![]() отрицателен (a
– острый угол и поэтому
отрицателен (a
– острый угол и поэтому ![]() )
и корнями уравнения
)
и корнями уравнения ![]() будут
будут ![]() и
и 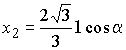 ,
то
,
то ![]() положительно
на
положительно
на 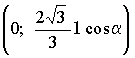 и
отрицательно на
и
отрицательно на 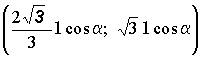 .
Поэтому на указанных двух промежутках функция V(x) соответственно
возрастает и убывает, а значит, при
.
Поэтому на указанных двух промежутках функция V(x) соответственно
возрастает и убывает, а значит, при 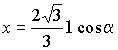 на промежутке
на промежутке ![]() функция V(x) принимает наибольшее значение.
функция V(x) принимает наибольшее значение.
Ответ: 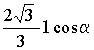 .
.
Упражнение 7.2.18. (КубГУ, эконом., 1990 г.)
У правильной четырехугольной пирамиды боковые ребра равны 5 см, а высота – 3 см. В эту пирамиду вписываются всевозможные пирамиды с вершинами в центре ее основания и с основаниями, являющимися ее плоскими сечениями, перпендикулярными к высоте. Найти высоту той из вписанных пирамид, объем которой наибольший.
Указание. Как и в примере 7.2.17 приводим задачу к нахождению x (x – высота вписанной пирамиды), при котором функция V(x) (объем вписанной пирамиды) принимает наибольшее значение на промежутке (0;3).
Ответ: 1 см.