Для прямоугольного параллелепипеда имеют место равенства V = abc и ![]() ,
,
где V – объем; a = AB;
b = AD; ![]() ;
; ![]() (докажите второе равенство!).
(докажите второе равенство!).
 |
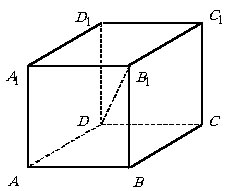
Отрезок, соединяющий вершины параллелепипеда, не лежащие на одной грани,
называется диагональю параллелепипеда.
Для прямоугольного параллелепипеда имеют место равенства V = abc и |
Диагональ прямоугольного параллелепипеда равна 9, а диагонали каких-то
двух граней равны ![]() и
и ![]() . Найти
объем параллелепипеда. Ответ: 112.
. Найти
объем параллелепипеда. Ответ: 112.
@
Многоугольник, вершины которого являются точками пересечения прямых, проходящих
через боковые ребра призмы, и плоскости, перпендикулярной к этим прямым,
называют перпендикулярным сечением
призмы. Ясно, что любые два перпендикулярных
сечения призмы –равные многоугольники, так как один из них получается из
другого в результате параллельного переноса вдоль прямой, содержащей боковое
ребро.
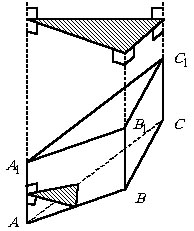 |
Следует различать
два понятия: перпендикулярное сечение и сечение, перпендикулярное ребру
призмы. Так, на рисунке вверху заштриховано перпендикулярное сечение призмы |
|
|
(1)
|
| S бок = P^сеч Ч1, |
(2)
|
| V = S осн Чh, |
(3)
|
| V = S^сеч Ч1, |
(4)
|
S бок – площадь боковой поверхности, являющейся объединением всех боковых граней призмы;
S осн – площадь одного из оснований призмы;
P^сеч и S^сеч – соответственно периметр и площадь перпендикулярного сечения призмы;
1 – длина бокового ребра;
V – объем призмы;
h – высота призмы.
Для прямой призмы 1 = h и многоугольник в основании равен перпендикулярному сечению, а значит
где P осн – периметр одного из оснований этой прямой призмы.
Пример 7.1.2. (КубГУ, физич., 1990 г.)
Объем правильной треугольной призмы равен V. Угол между диагоналями двух граней, проведенными из одной и той же вершины, равен a. Найти сторону основания призмы.
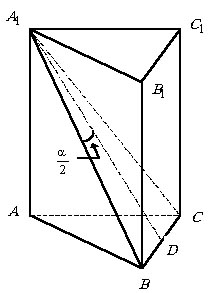 |
Медиана AD равнобедренного треугольника 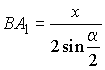 .
Отсюда из прямоугольного треугольника .
Отсюда из прямоугольного треугольника |
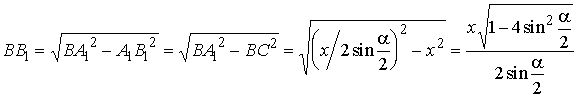 .
.
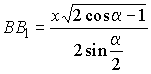 .
.
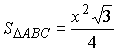 ,
по формуле (6) получаем
,
по формуле (6) получаем
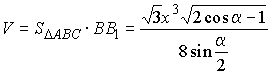 .
.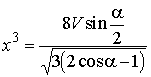 или
или 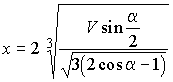 .
.
Ответ: 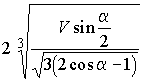 .
.
Краткая схема решения примера 7.1.2 выглядит следующим образом: сначала
из ![]() через
x и a
выразили
через
x и a
выразили ![]() ,
затем из
,
затем из ![]() через x и a
выразили
через x и a
выразили ![]() , далее из DABC
через x выразили Sосн
, далее из DABC
через x выразили Sосн ![]() ,
и наконец, по формуле (6) V = S осн
Ч1 получили уравнение
относительно x. Следует отметить, что как и в примере 7.1.2 большинство
стереометрических конкурсных заданий удается свести к решению некоторых
простейших планиметрических задач.
,
и наконец, по формуле (6) V = S осн
Ч1 получили уравнение
относительно x. Следует отметить, что как и в примере 7.1.2 большинство
стереометрических конкурсных заданий удается свести к решению некоторых
простейших планиметрических задач.
Упражнение 7.1.3.
В основании прямой призмы лежит равнобедренный треугольник с углом 120° и боковой стороной a. Острый угол между скрещивающимися диагоналями боковых граней, проходящих через боковые стороны основания, равен a. Найти объем призмы.
Указание.
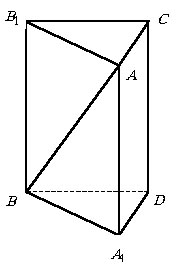
На рисунке ![]() – исходная прямая призма, у которой AB = BC = a, РABC
= 120°
и угол между скрещивающимися прямыми
– исходная прямая призма, у которой AB = BC = a, РABC
= 120°
и угол между скрещивающимися прямыми ![]() и
и ![]() равен a.
равен a.
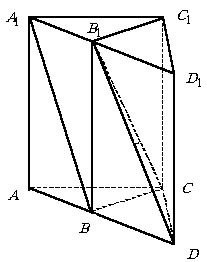 |
Достроим к этой призме еще одну правильную призму Так как |
Ответ: 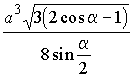 .
.
В указании к решению упражнения 7.1.3 мы построили призму, о которой не упоминалось в условии задания, что позволило несколько упростить само решение. В следующем примере рассмотрим ситуацию, когда в условии задания вообще не идет речь о призме, но тем не менее ее построение опять облегчает подход к решению задания.
Пример 7.1.4. (КубГУ, матем., 1995 г.)
Концы отрезка АВ лежат на гранях двугранного угла, равного 60°. Из точек А и В опущены перпендикуляры АС и ВD на ребро двугранного угла. Найти АС, если CD = 24 см, BD = 8 см, AB = 25 см.
 |
Согласно условию задания мы можем построить прямую призму (см. рисунок),
у которой
Далее, полагая AC = x, из |
т.е. ![]() или
или ![]() .
Отсюда
.
Отсюда ![]() (см) и
(см) и ![]() (см).
(см).
Ответ: 3 или 5 см.
Упражнение 7.1.5.
В пространстве даны четыре точки А, В, С и D так, что AB = 1, CD = 2, BC = 3 и AD = 4, причем прямые АВ и CD перпендикулярны к прямой ВС. Найти величину двугранного угла с ребром ВС между полуплоскостями, содержащими треугольники АВС и BCD.
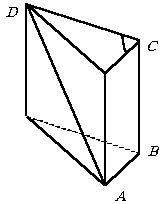 |
Указание. Сначала докажите, что точки А, В, С и D не могут лежать в одной плоскости. Это будет обоснованием того, что можно, как указано на рисунке, построить прямую призму, у которой a – искомый угол. |
Наиболее часто в конкурсных заданиях рассматривают сечения призмы различными плоскостями. При решении такого рода заданий необходимо уметь строить эти сечения и обосновывать свои построения. Для иллюстрации приведем пример.
Пример 7.1.6. (КубГУ, матем., 1992 г.)
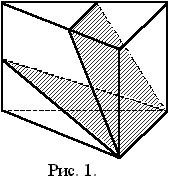
В правильной треугольной призме высота и сторона основания равны a . Через сторону основания проведена плоскость, составляющая с плоскостью основания угол 60°. Найти периметр полученного сечения.
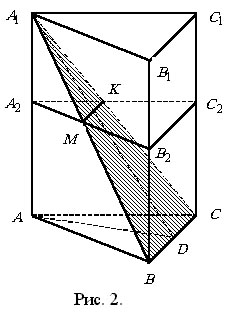 |
Как видно из рисунка 1, при решении этого задания очень важно выяснить
вид сечения – треугольник или четырехугольник? Для этого, например, сначала
построим правильную призму В равностороннем треугольнике АВС находим медиану 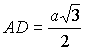 и из прямоугольного
и из прямоугольного
треугольника 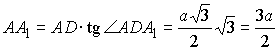 . .
|
Далее, так как всякая плоскость пересекает параллельные плоскости по параллельным
прямым, то ![]() ,
, ![]() и MK ||BC.
Отсюда следует, что ВМКС – трапеция и
и MK ||BC.
Отсюда следует, что ВМКС – трапеция и ![]() подобен
подобен ![]() ,
в частности,
,
в частности, ![]() .
Из прямоугольного треугольника
.
Из прямоугольного треугольника ![]() по теореме Пифагора находим
по теореме Пифагора находим
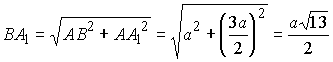 .
.
Так как ![]() ,
то из подобия треугольников
,
то из подобия треугольников ![]() и
и ![]() получаем
получаем
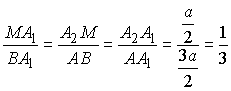 .
.
Отсюда ![]() и
и
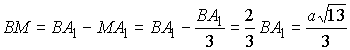 .
.
Аналогично из треугольника ![]() (как и из треугольника
(как и из треугольника ![]() )
можем получить
)
можем получить 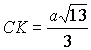 (в частности, ВМКС – равнобедренная трапеция). Теперь окончательно
находим периметр сечения ВМКС
(в частности, ВМКС – равнобедренная трапеция). Теперь окончательно
находим периметр сечения ВМКС
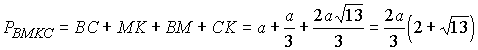 .
.
Ответ: 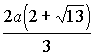 .
.
Замечание к решению примера 7.1.6. В условии не требовалось устанавливать, что сечение – равнобедренная трапеция. Тем не менее в большинстве конкурсных заданий приходится определять с обоснованием вид сечения. Также следует отметить, что указанный способ определения вида сечения является далеко не единственным, хотя достаточно аргументированным.
Упражнение 7.1.7.
В правильной треугольной
призме боковое ребро и сторона основания равны a. Через среднюю
линию основания проведена плоскость, составляющая с плоскостью основания
угол 60°.
Найти периметр полученного сечения.
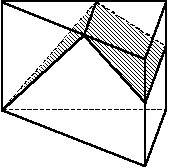 |
Указание. Обоснуйте возможность двух вариантов расположения сечения: оно может быть треугольником или трапецией (см. рисунок). |
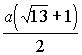 или
или 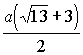 .
.
Теперь перейдем к рассмотрению
одной очень важной формулы, связывающей площади плоской фигуры и ее ортогональной
проекции на плоскость. Как правило, эта формула наиболее часто применима
при решении задач на призму.
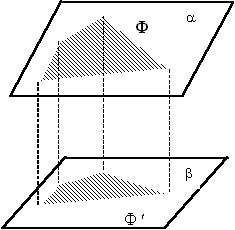 |
Ортогональной проекцией фигуры (или
тела) на данную плоскость называют множество точек пересечений с этой плоскостью
перпендикулярных к ней прямых, проходящих через все точки этой фигуры (или
тела). Если фигура Ф с площадью S лежит в плоскости a,
а фигура
|
В случае 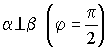
![]() вырождается (полагаем
вырождается (полагаем ![]() ),
а в случае a || bили
a = b (
f = 0)
имеем Ф =
),
а в случае a || bили
a = b (
f = 0)
имеем Ф = ![]() (очевидно,
(очевидно, ![]() ).
).
Пример 7.1.8. (КубГУ, физич., 1990 г.)
Основанием прямой четырехугольной призмы служит ромб с острым углом a. Под каким углом к плоскости основания надо провести плоскость, чтобы получить в сечении квадрат с вершинами на боковых ребрах призмы?
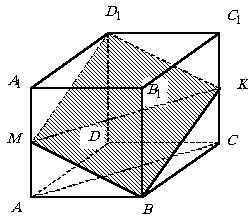 |
Будем считать, что упоминаемую в условии задания плоскость можно провести.
Не ограничивая общности рассуждений, полагаем, что две вершины квадрата
в сечении совпадают с вершинами призмы (см. рисунок, вершины В и |
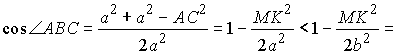
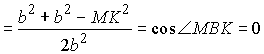 (учли, что РMBK
=90° ).
Получили cos РABC
< 0,
т.е. РABC
– тупой и, следовательно, РBAD
= a
– острый, тогда РABC
= p - a.
Далее, по теореме косинусов из треугольника АВС находим
(учли, что РMBK
=90° ).
Получили cos РABC
< 0,
т.е. РABC
– тупой и, следовательно, РBAD
= a
– острый, тогда РABC
= p - a.
Далее, по теореме косинусов из треугольника АВС находим ![]() .
.
Из прямоугольного треугольника МВК находим ![]() ,
откуда ввиду AC = MK получаем равенство
,
откуда ввиду AC = MK получаем равенство ![]() .
Поэтому
.
Поэтому ![]() и
и ![]() .
.
Учитывая, что ромб ABCD – ортогональная
проекция квадрата ![]() ,
и обозначая через b
угол между плоскостью сечения и плоскостью основания, по формуле (7) получаем
,
и обозначая через b
угол между плоскостью сечения и плоскостью основания, по формуле (7) получаем
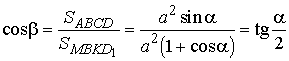 ,
т.е.
,
т.е.  .
.
Ответ: 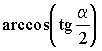 .
.
Замечание к
решению примера 7.1.8. Ясно, что рассматриваемая в решении призма со стороной
основания a имеет наименьшую
высоту, когда в сечении можно получить квадрат с вершинами на всех боковых
ребрах призмы. В качестве упражнения следует вычислить высоту этой призмы
(она равна 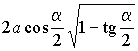 ).
Поэтому более точно в примере 4 ответ должен звучать так: если отношение
высоты призмы к стороне основания меньше числа
).
Поэтому более точно в примере 4 ответ должен звучать так: если отношение
высоты призмы к стороне основания меньше числа 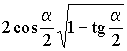 ,
то ни под каким углом к плоскости основания требуемую в условии задания
плоскость провести нельзя; если же указанное отношение не меньше этого
числа, то искомый угол будет равен
,
то ни под каким углом к плоскости основания требуемую в условии задания
плоскость провести нельзя; если же указанное отношение не меньше этого
числа, то искомый угол будет равен 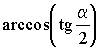 .
.
Пример 7.1.8 без особого труда можно решить, не используя формулу (7). Приведем задание, в котором использование этой формулы является необходимым.
Упражнение 7.1.9.
Ребро АВ призмы – сторона основания и сторона прямоугольника, являющегося
боковой гранью этой призмы. Двугранный угол призмы при ребре АВ
является острым. Под углами в 30° и 45° к основанию
через ребро АВ проведены две плоскости, пересекающие все боковые
ребра призмы. Площади полученных сечений призмы соответственно равны ![]() кв. ед. и
кв. ед. и ![]() кв. ед. Найти отношение высоты призмы к длине ее бокового ребра.
кв. ед. Найти отношение высоты призмы к длине ее бокового ребра.
Указание. Через
АВ проведем плоскость перпендикулярно к грани, являющейся прямоугольником.
Она пересечет прямые, содержащие боковые ребра призмы, в вершинах ее перпендикулярного
сечения, которое будет ортогональной проекцией на эту плоскость основания
и двух сечений призмы.
 |
Обозначая через f
угол между плоскостью основания и плоскостью перпендикулярного сечения,
получим рисунок для линейных углов, стороны которых соответствуют указанным
на рисунке плоскостям.
Согласно формуле (7) получаем равенства
|
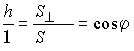 .
.Ответ: ![]() .
.
Перейдем к иллюстрациям построений плоских сечений многогранников методом
следов. Секущая многогранник плоскость пересекает некоторую плоскость
w по прямой линии, называемой следом
секущей плоскости на w.
В качестве w
часто рассматривают грани многогранника, и тогда следы секущей плоскости
на плоскостях, проходящих через грани, дают представление о виде сечения.
Пример 7.1.10.
Построить сечение куба ![]() плоскостью, проходящей через середины ребер
плоскостью, проходящей через середины ребер ![]() и
и ![]() и вершину
С.
и вершину
С.
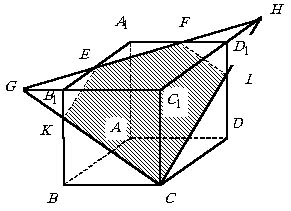 |
Пусть Е и F – соответственно
середины ребер |
Упражнение 7.1.11. (КубГУ, ФПМ, 1990 г.)
При условии примера 7.1.10 найти площадь сечения, если ребро куба равно a.
Указание. Найдите площадь двумя способами. Первый способ: искомая площадь равна сумме площадей трапеции KEFL и треугольника KCL. Второй способ: найдите площадь ортогональной проекции сечения на основание и используйте формулу (7).
Ответ: 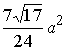 .
.
При
построении сечений многогранников полезны следующие утверждения: 1) если
точки А и В лежат на плоскости w,
то и прямая АВ лежит на w;
2) если прямая ![]() параллельна плоскости w
и плоскость, проходящая через
параллельна плоскости w
и плоскость, проходящая через ![]() ,
пересекает w
по прямой
,
пересекает w
по прямой ![]() ,
то
,
то ![]() ; 3)
прямые пересечения параллельных плоскостей с данной плоскостью тоже параллельны.
; 3)
прямые пересечения параллельных плоскостей с данной плоскостью тоже параллельны.
Утверждение 1) мы уже использовали при построении сечения в примере 7.1.10. Приведем пример, иллюстрирующий применение утверждений 2) и 3).
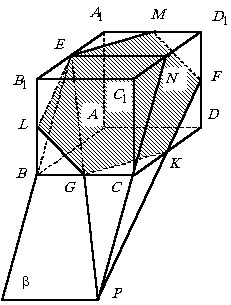
Пример 7.1.12.
В кубе ![]() на ребрах
на ребрах ![]() ,
, ![]() и ВС взяты точки Е, F
и G соответственно. Построить
сечение куба плоскостью, проходящей через Е, F
и G.
и ВС взяты точки Е, F
и G соответственно. Построить
сечение куба плоскостью, проходящей через Е, F
и G.
Через a
обозначим секущую плоскость. Прежде чем находить следы плоскости a
на грани куба, построим дополнительную плоскость b,
которая проходит через точки Е, G
и C. Так как прямая СВ
параллельна грани ![]() ,
то b пересекает
эту грань по прямой EN (см.
рисунок), параллельной СВ. Прямые EG
и NC лежат в плоскости b
и пересекаются в некоторой точке Р. Так как прямая EG
– след a
на b,
то Р принадлежит a.
,
то b пересекает
эту грань по прямой EN (см.
рисунок), параллельной СВ. Прямые EG
и NC лежат в плоскости b
и пересекаются в некоторой точке Р. Так как прямая EG
– след a
на b,
то Р принадлежит a.
 |
Но Р принадлежит
прямой NC , лежащей на плоскости
грани Далее мы могли бы аналогично найти точки пересечения плоскости a с ребрами |
Упражнение 7.1.13. (КубГУ, ФПМ, 1990 г.)
При условии примера 7.1.12 и с учетом того, что Е, F и G – середины соответствующих ребер и a – длина ребра куба, доказать правильность шестиугольника EMFKGL и найти его площадь.
Указание. При доказательстве правильности шестиугольника недостаточно показать равенство его сторон, надо также показать равенство его углов.
Ответ: ![]() .
.