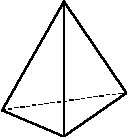
Рис. 1.
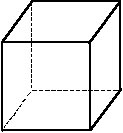
Рис. 2.
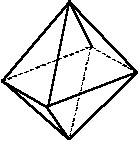
Рис. 3.
где В – число вершин, Р – число ребер и Г – число граней многогранника.
Проверьте эту формулу на известных Вам многогранниках. Справедлива ли она для многогранника, являющегося кубом, у которого изнутри удален маленький кубик?
Упражнение 7.0.1.
В выпуклом многограннике каждая грань является n-угольником и из каждой вершины выходит m ребер. Доказать, что m Ј 5 и n Ј 5.
Указание. Используйте формулу Эйлера и равенства nГ = mB = 2P (которые необходимо обосновать!).
Выпуклый многогранник называют правильным, если все его грани являются
равными друг другу правильными многоугольниками и из каждой вершины выходит
одинаковое число ребер. Оказывается, что у правильного многогранника все
двугранные углы тоже равны и с точностью до подобия существует всего пять
правильных многогранников: правильный тетраэдр (четыре грани – треугольники,
рис. 1), куб или гексаэдр (шесть граней – квадраты, рис. 2), правильный
октаэдр (восемь граней – треугольники, рис. 3), додекаэдр (двенадцать граней
– пятиугольники, рис. 4) и икосаэдр (двадцать граней – треугольники, рис.
5):

Рис. 1. |

Рис. 2. |

Рис. 3. |
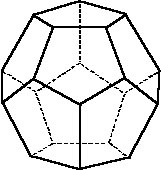
Рис. 4. |
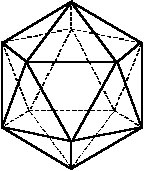
Рис. 5. |
Используя формулу Эйлера и рассуждения при доказательстве предыдущего упражнения, попытайтесь обосновать, что число граней у правильного многогранника может быть равно только одному из чисел: 4, 6, 8, 12 или 20.
Перейдем к рассмотрению многогранников, наиболее часто встречающихся на
вступительных экзаменах по математике: призмам, пирамидам и усеченным пирамидам.