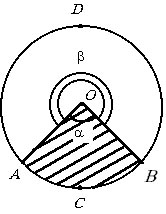
@ На рисунке изображено два центральных угла: величиной a, опирающийся на дугу ACB, и величиной b, опирающийся на дугу ADB. Говорят, что дуга ACB имеет угловую величину a, а дуга ADB имеет угловую величину b, и при этом пишут ИACB = a, ИADB = b. Если R – радиус окружности, то длина окружности равна 2 pR. Если a – градусная мера угла, то длина дуги ACB равна , если же a – радианная мера угла, то длина дуги ACB равна Ra.

      Площадь круга равна , а площадь сектора, опирающегося на дугу ACB, равна , если a – градусная мера, и , если a – радианная мера. Ясно, что угловые величины дуг рассматриваются только от 0° до 360° (от 0 радиан до 2 p радиан). Отношение угловых величин дуг равно отношению их длин, а также отношению площадей секторов, опирающихся на эти дуги. В частности, на одной и той же окружности, дуга с большей угловой величиной имеет большую длину, а дуги с равными угловыми величинами имеют равные длины.

Пример 6.7.1.

      На окружности даны две дуги с угловыми величинами a и b. Найти отношение длин хорд, стягивающих эти дуги.

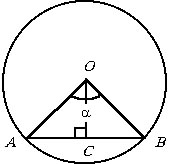
Пусть R – радиус окружности и AB – хорда, стягивающая дугу, величиной a. В равнобедренном треугольнике AOB проведем высоту (медиану и биссектрису) OC. Из DAOC находим  (первый рисунок) и         (второй рисунок).   Во всех случаях .

      Аналогично найдем длину хорды, стягивающей дугу, величиной b –  . Откуда окончательно можем

найти отношение длин этих хорд .

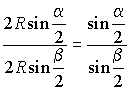Ответ: .

Пример 6.7.2.

      Дана окружность и две ее хорды, отношения которых к диаметру окружности соответственно равны a и b. Найти отношение длин меньших дуг, стягиваемых этими хордами.

Отношение длин дуг равно отношению их угловых величин. Поэтому достаточно определить угловые величины меньших дуг, стягиваемых хордами.
 

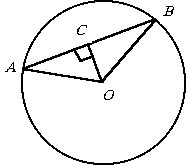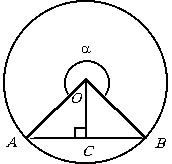
Пусть R – радиус окружности, AB – первая из рассматриваемых хорд и OC – высота равнобедренного треугольника с вершиной в центре окружности O. По условию . Ясно, что , т.е. РAOB = 2 arcsin a  и поэтому РAOС = 2 arcsin a.

      Аналогично найдем угловую величину меньшей дуги, стягиваемой второй хордой. Она будет равна 2 arcsin b. Откуда окончательно находим .

Ответ: .

@ Большую роль в решении задач по теме “Окружность” играют вписанные углы.
 

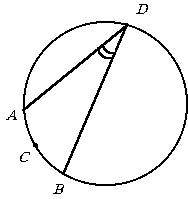Известно, что вписанный угол равен половине угловой величины дуги, на которую он опирается. Так как на рисунке угол ADB является вписанным, поэтому . Ясно, что вписанный угол, опирающийся на диаметр (на дугу в 180° ), является обязательно прямым, а любые два вписанных угла, опирающихся на одну и ту же дугу, будут равными.

Пример 6.7.3. (КубГУ, матем., 1986 г.)

      В окружности проведены хорды AB и AC, причем AB = 2 см, AC = 1 см, РCAB = 120° . Найти длину той хорды окружности, которая делит РCAB  пополам.

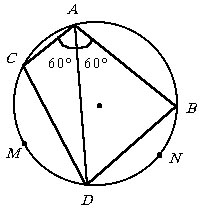Пусть AD – хорда, делящая угол CAB пополам и x – ее длина. Дуги CMD и BND (см. рисунок) равны по 120° , т.к. опирающиеся на них вписанные углы CAD и BAD равны по 60° . Поэтому хорды CD и BD, стягивающие равные дуги, тоже равны. Положим CD  = BD = y. По теореме косинусов для треугольников ACD и ABD имеем  и , т.е.  и . Вычитая из первого равенства второе, находим 0 = -3 + x и x = 3.

Пример 6.7.4.

      В треугольнике ABC точка D лежит на стороне CB, причем AB = 12, AC = 15 и AD = 10. Найти сторону BC, если известно, что окружность, описанная около треугольника ADC, касается прямой AB.

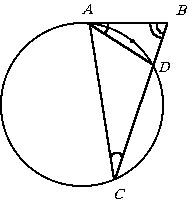Ясно, что A – точка касания окружности и прямой AB. Имеем . И так как РB – общий в треугольниках BAD и BCA, то эти треугольники по третьему признаку подобны, а значит из пропорции , учитывая AB = 12, AC = 15 и AD = 10, находим .

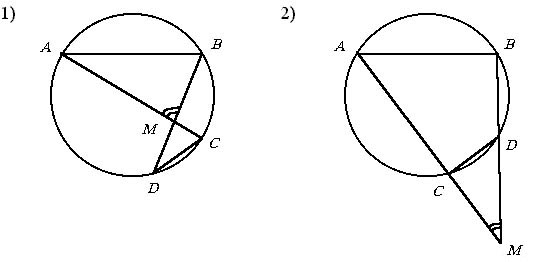
@ Очень полезным в рассматриваемой теме является умение определять углы между хордами и между секущими к окружности.

       На первом рисунке угол g между хордами AC и BD является внешним для треугольника DMC, а значит, равен сумме не смежных с ним углов MDC и MCD.

Так как  и , то окончательно получаем .

На втором рисунке угол g между секущими AB и AC равен разности внешнего угла BMC треугольника AMB и угла ABM, и поэтому , т.е. .

Пример 6.7.5.

      Пусть AB и CD – непересекающиеся хорды данной окружности, причем AB является стороной квадрата, а CD – стороной правильного шестиугольника, вписанных в окружность.
      Найти острый угол между прямыми AC и BD.

      Меньшие дуги, стягиваемые хордами AB и CD, соответственно равны 90°  и 60° .
      Выделим четыре возможных случая расположения точек A, B, C , D на окружности:

 

1) В этом случае РAMB равен полусумме угловых величин меньших дуг AB и CD (угол между хордами), т.е. .

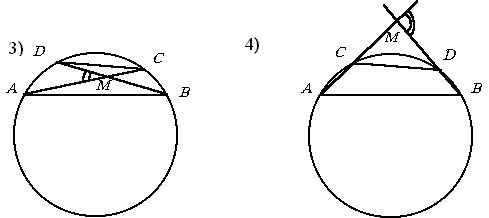
      2) В этом случае РAMB равен полуразности угловых величин меньших дуг AB и CD (угол между секущими), т.е. .

      3) В этом случае РAMB равен полусумме угловых величин меньшей дуги CD и большей дуги AB, т.е. , а значит острый угол между хордами AC и BD равен 180° - 165° = 15°.

     4) В этом случае РAMB равен полуразности угловых величин большей дуги AB и меньшей дуги CD, т.е. , а значит острый угол между прямыми AC и BD равен 180° - 105° = 75°.
     Заметим, что, не ограничивая общности рассуждений, мы рассмотрели все случаи.

      Ответ: 15°  или 75°.

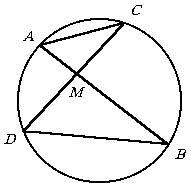
@  При решении задач на окружность удобно использовать равенство AM ЧMB = CM ЧMD, которое выполняется для любых хорд AB и CD с точкой их пересечения M. Это равенство непосредственно следует из подобия треугольников AMC и DMB. Причем, если точка M отстоит от центра окружности радиуса R на расстоянии, равном d , то имеет место соотношение .        Другое, но также часто используемое соотношение в конкурсных задачах, , где AB – отрезок касательной к окружности, BC – секущая к окружности, пересекающая окружность в точке D. Попробуйте доказать самостоятельно это соотношение, а также соотношение  для всякой точки М, расположенной вне окружности радиуса R и отстоящей от центра этой окружности на расстоянии, равном d , проведя рассуждения, подобные рассуждениям при решении примера  6.6.4.

 
 
Пример 6.7.6.

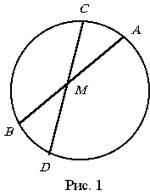
      Хорды AB и CD данной окружности имеют длины соответственно 4 и 1. Прямые AB и CD пересекаются в точке М так, что AM= 2. Найти max(CM, DM).

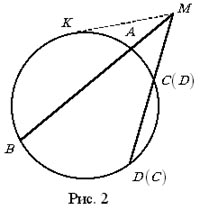Сначала предположим, что прямые AB и CD пересекаются внутри окружности (рис. 1). Полагая CM = x и учитывая BM = AB - AM = 2, имеем равенство AM ЧMB = CM ЧMD, т.е. 2 Ч1 = x(2 - x) или . Но дискриминант этого уравнения равен -4 < 0, а значит, эта ситуация невозможна. Поэтому прямые AB и CD могут пересекаться только во внешней точке окружности (рис. 2).        Так как max(CM, DM) равен длине всего отрезка секущей независимо от обозначения концов меньшей хорды буквами C и D, то для определенности можем положить, что точка С лежит между точками М и D. Тогда max(CM, DM) = MD. Из точки М проведем касательную к окружности, которая касается окружности в точке К.         Из рассуждений, предшествующих примеру 6.7.6, имеем, с одной стороны, , с другой стороны, , т.е. MA ЧMB = MC ЧMD.

      Учитывая, согласно условию AM = 2, AB = 4, CD = 1 и полагая MC = x, получаем MB = 6 и MD = x + 1, а значит, 2 Ч6 = x(x + 1). Откуда следует . Ввиду x > 0 находим x = 3 и поэтому MD = x + 1 = 4.

      Ответ: 4.

Пример 6.7.7.

      Из точки А к окружности радиуса R проведена касательная, которая касается окружности в точке М. Секущая, проходящая через точку А, пересекает окружность в точках К и N, причем N – середина отрезка AK, угол АМК равен N. Найти площадь треугольника АМК.

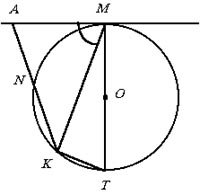Проведем диаметр МТ. Тогда РKMT = 30°  и из прямоугольного треугольника МКТ находим  .        Пусть AN = NK = x, тогда AK = 2x. Используя соотношение , найдем . Применим теорему косинусов к стороне АК треугольника АМК.

 ,,

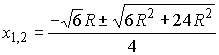, т.к. x > 0, то ,

тогда .

      Окончательно , .

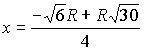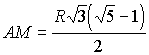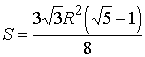      Ответ: 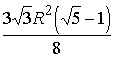.