ВПЕРЕД
| НАЗАД | ГЛАВНАЯ
| ПЛАНИМЕТРИЯ | СТЕРЕОМЕТРИЯ
6.8. Многоугольники
@
Согласно школьному курсу математики под n - угольником понимают n - звенную
замкнутую ломаную либо часть плоскости, ограниченной такой ломаной. Вершины
и звенья ломаной называют соответственно вершинами и сторонами многоугольника.
Для определенности в дальнейшем мы будем рассматривать многоугольник как
часть плоскости.
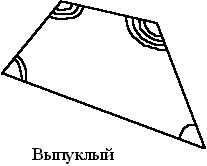

|
Многоугольник (и вообще
любую фигуру) называют выпуклым, если для любых его двух точек отрезок
с концами в этих точках полностью принадлежит многоугольнику (фигуре).
В частности, треугольник и круг – выпуклые фигуры, а граница треугольника
(трехзвенная замкнутая ломаная) и окружность – невыпуклые фигуры.
Многоугольник является
выпуклым тогда и только тогда, когда все его внутренние углы меньше 180°
(см. рисунок). Выпуклый многоугольник всегда расположен в одной полуплоскости
относительно каждой прямой, проходящей через его сторону. Имеются полезные
утверждения, которые справедливы для многоугольников независимо от того,
выпуклы они или нет: |
1. Сумма внутренних углов
n-угольника (n і 3)
равна 180°
(n - 2).
2. n-угольник (n і
4)
имеет ровно 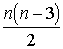 диагоналей (под диагональю многоугольника понимают отрезок, соединяющий
любые его две несмежные вершины).
диагоналей (под диагональю многоугольника понимают отрезок, соединяющий
любые его две несмежные вершины).
3. Если 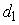 и
и 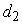 – длины
диагоналей четырехугольника, а a
– угол между прямыми, проходящими через эти диагонали, то площадь четырехугольника
равна
– длины
диагоналей четырехугольника, а a
– угол между прямыми, проходящими через эти диагонали, то площадь четырехугольника
равна 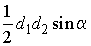 .
.
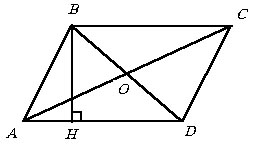
4. Если прямые, содержащие
диагонали четырехугольника, перпендикулярны, то суммы квадратов его противоположных
сторон равны.
Попробуйте доказать первое из этих утверждений хотя бы для невыпуклых 4-
и 5- угольников, второе – для любых многоугольников, третье – для
невыпуклого четырехугольника, а четвертое – для любого четырехугольника.
Пример 6.8.1.
Внутренние углы многоугольника образуют геометрическую прогрессию 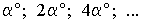 Определить наибольшее возможное число диагоналей такого многоугольника.
Определить наибольшее возможное число диагоналей такого многоугольника.
Решение
В таком n - угольнике
сумма внутренних углов равна 180°
(n - 2), а с другой стороны, как
сумма членов геометрической прогрессии равна 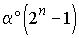 .
Откуда находим
.
Откуда находим 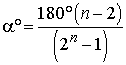 .
.
Так как наибольший угол 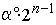 должен быть меньше 180°
, то имеем
должен быть меньше 180°
, то имеем 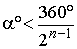 .
Приходим к неравенству
.
Приходим к неравенству 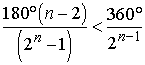 ,
которое после преобразований принимает вид
,
которое после преобразований принимает вид
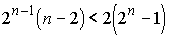 или
или 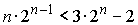 .
.
Замечаем, что при n і 6
имеем 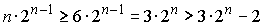 ,
а значит, n Ј 5.
,
а значит, n Ј 5.
Легко проверить, что n
= 5 соответствует условию (существует пятиугольник, у которого a°
= (540/31)° ). При n = 5 находим количество диагоналей 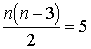 .
.
Ответ: 5.
@
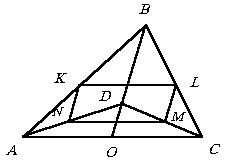
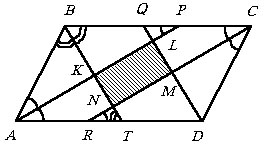
Интересным и полезным является следующее соображение: четырехугольник,
вершины которого являются серединами сторон данного четырехугольника, будет
параллелограммом с площадью вдвое меньшей площади данного четырехугольника.
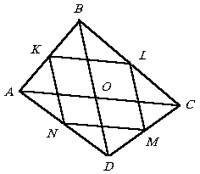
|
Действительно, независимо от того, выпуклый или невыпуклый данный четырехугольник
ABCD (см. рисунок), KL и NM – средние линии треугольников ABC и ADC, а
значит, они равны половине АС и параллельны прямой АС. Откуда следует,
что KLMN – параллелограмм.
Аналогично можно показать,
что KN = LM = 1/2 BD, KN ззBD
и LM ззBD. Площадь
параллелограмма равна произведению длин его сторон на синус угла между
ними, т.е. 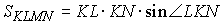 . .
Учитывая, что KL = 1/2
AC, KN = 1/2 BD и sin РLKN
= sin РAOB
(углы LKN и AOB являются углами с взаимно параллельными сторонами), получаем
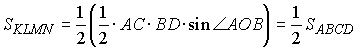 , , |
(воспользовались утверждением
3 в начале этого параграфа).
Пример 6.8.2.
(КубГУ, эконом., 1994 г.)
Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника
равны 4 см и 6 см, одна из его диагоналей равна 8
см. Вычислить площадь четырехугольника.
Решение
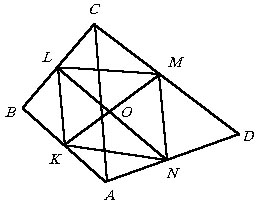 |
Пусть KN = 4,
LN = 6 и AC = 8. Тогда 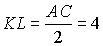 как средняя линия треугольника ABC.
Если O – точка пересечения KM
и LN, то в силу ранее отмеченного,
что KLMN – параллелограмм, находим
как средняя линия треугольника ABC.
Если O – точка пересечения KM
и LN, то в силу ранее отмеченного,
что KLMN – параллелограмм, находим 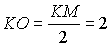 и
и 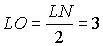 . .
Ясно, что площадь параллелограмма KLMN
в четыре раза больше площади треугольника KOL
(покажите самостоятельно!), а площадь четырехугольника ABCD
ввиду ранее отмеченного вдвое больше площади параллелограмма KLMN,
т.е. 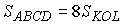 . . |
По формуле Герона находим 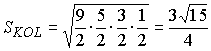 ,
и поэтому
,
и поэтому 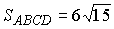 (см
(см ).
).
Ответ: 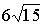 см
см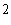 .
.
Теперь приведем пример решения задачи с использованием утверждения 4 в
начале этого параграфа.
Пример 6.8.3.
Сторона AB четырехугольника
ABCD равна 9, другие
стороны тоже измеряются натуральными числами. Найти остальные стороны четырехугольника,
если известно, что его диагонали AC
и BD перпендикулярны и 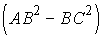 – простое число.
– простое число.
Решение
Так как диагонали перпендикулярны, то согласно утверждению 4 имеем 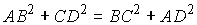 (это равенство получите самостоятельно по теореме Пифагора независимо от
того, выпуклый или невыпуклый четырехугольник ABCD).
Откуда следует
(это равенство получите самостоятельно по теореме Пифагора независимо от
того, выпуклый или невыпуклый четырехугольник ABCD).
Откуда следует 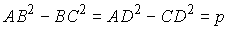 – простое число. Это возможно лишь в случае, когда AB - BC = 1,
AB + BC = p, AD - CD = 1 и AD
+ CD = p. Учитывая, что AB = 9, находим BC = 8 и p
= 17, а значит, AD = 9 и CD = 8.
– простое число. Это возможно лишь в случае, когда AB - BC = 1,
AB + BC = p, AD - CD = 1 и AD
+ CD = p. Учитывая, что AB = 9, находим BC = 8 и p
= 17, а значит, AD = 9 и CD = 8.
Ответ: AD = 9 , BC = CD = 8.
@
Для решения задач на многоугольники полезно выучить и уметь объяснять следующие
простейшие соотношения, многие из которых мы уже ранее использовали.
Параллелограмм
 |
AB ззCD
и AB = CD; AO = OC
и O – центр симметрии;
DABC
= DCDA
и DAOB
= DCOD;
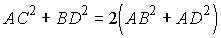 ; ;
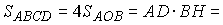
= AB Ч AD Ч
sin РBAD =
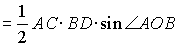 . . |
Если AB = AD, то ABCD – ромб,
AC ^BD
и 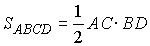 .
.
Если РBAD
= 90°, то ABCD – прямоугольник и 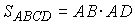 .
.
Если AB = AD и РBAD
= 90°, то ABCD – квадрат и обладает
всеми свойствами ромба и прямоугольника.
Трапеция
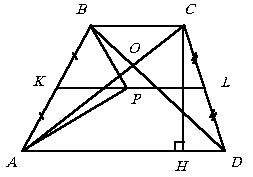 |
Здесь AD > BC и AD, BC – основания, AD ззBC
и AB ззCD ,
KL – средняя линия и 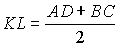 ; ;
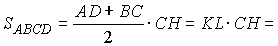
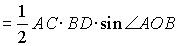 ; ; |
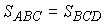 ,
, 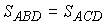 и
и 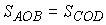 ; DAOD
подобен DCOB
с коэффициентом подобия
; DAOD
подобен DCOB
с коэффициентом подобия 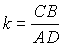 ,
CO = k ЧAO,
OB = k ЧOD
и
,
CO = k ЧAO,
OB = k ЧOD
и 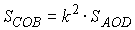 .
.
Если AP и BP – биссектрисы углов A и B, то РAPB
= 90° и точка P лежит на прямой KL
(см. рассуждения ниже в начале решения примера 6.8.4).
Если AB
= CD, то ABCD – равнобедренная трапеция
и 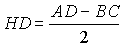 , а
если к тому же AC ^BD,
то
, а
если к тому же AC ^BD,
то 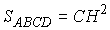 .
.
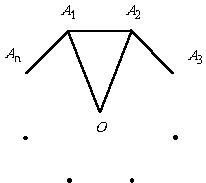
Правильные n
- угольники
 |
@
Все стороны равны и все углы равны; можно вписать и описать окружности,
причем их центры совпадают (точка O).
Если R и r – соответственно
радиусы вписанной и описанной окружности, то
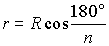 |
и 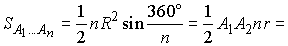
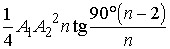 ;
;
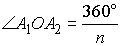 и
и 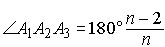 ;
;
при n=6 имеем 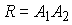 и
и 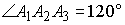 .
.
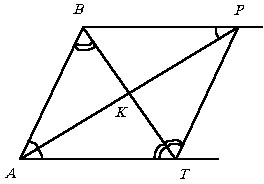
Пример 6.8.4.
(КубГУ, физич., 1993 г.)
В параллелограмме со сторонами a и b и углом a
проведены биссектрисы четырех углов. Найти площадь четырехугольника, ограниченного
биссектрисами.
Решение
 |
Сначала рассмотрим некоторую конфигурацию, состоящую из прямых (см. рисунок),
на которой BP ззAT, BT
и AP – биссектрисы углов ABP
и BAT, К
– точка пересечения этих биссектрис.
Так как РBAP
= РPAT
и РPAT
= РBAP
(внутренние накрест лежащие углы), то DABP
– равнобедренный и AP = BP. |
Аналогично
устанавливаем, что AB = AT, а значит, ABPT
– ромб и К – его точка симметрии.
В частности, прямая, проходящая через К параллельно АТ, делит
любой отрезок, заключенный между прямыми АТ и ВP, пополам.
Заметим, что для решения задачи мы могли обойтись без этой конфигурации
и выбрать путь полегче. Однако проведенные рассуждения полезны тем, что
объясняют одно из ранее указанных простейших свойств трапеции.
Теперь перейдем к решению задачи. Тривиальные ситуации, когда все биссектрисы
пересекутся в одной точке либо две точки пересечения биссектрис лежат на
сторонах параллелограмма, исключим из рассмотрения. Возможны две ситуации
(см. рисунок).
 |
Для определенности положим AB = a, BC = b ( b > a),
РBAD = a.
Из ранее рассмотренной конфигурации прямых для наших рисунков можем сделать
следующие выводы: AB = BP = AT = a и аналогично CQ = CD = DR
= a, AP ^BT
и аналогично CR ^DQ,
т.е. KLMN – прямоугольник и 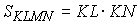 . . |
 Ясно, что РBPA
= РLPQ
= a/2,
QP = 2a - b
для верхнего рисунка и QP = b - 2a
для нижнего.
Ясно, что РBPA
= РLPQ
= a/2,
QP = 2a - b
для верхнего рисунка и QP = b - 2a
для нижнего.
Для верхнего рисунка имеем
KL = KP - PL
= BP cos РBPA
- QP cosРLPQ
=
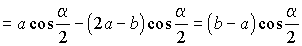 ,
,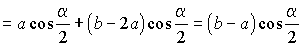 .
.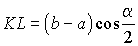 .
.
Аналогично, замечая, что  ,
в обоих случаях найдем
,
в обоих случаях найдем
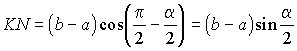 .
Откуда окончательно получаем
.
Откуда окончательно получаем
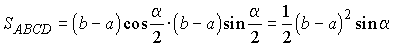 .
Теперь заметим, что при b = a биссектрисы пересекаются в одной точке
(получается вырожденный четырехугольник). Если считать a > b, то
ответ не изменится, а если вместо a
подставить в ответ p - a,
то получим равное число для площади четырехугольника (это говорит о том,
что если бы в качестве a
мы взяли тупой угол ABC, то
все равно имели бы такой же ответ).
.
Теперь заметим, что при b = a биссектрисы пересекаются в одной точке
(получается вырожденный четырехугольник). Если считать a > b, то
ответ не изменится, а если вместо a
подставить в ответ p - a,
то получим равное число для площади четырехугольника (это говорит о том,
что если бы в качестве a
мы взяли тупой угол ABC, то
все равно имели бы такой же ответ).
Ответ: 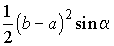 .
.
Теперь приведем одну задачу
о правильных многоугольниках, уже не раз встречавшуюся на устных и письменных
экзаменах по математике в КубГУ.
Пример 6.8.5.
В круг радиуса R
вписан правильный n - угольник, в этот n - угольник вписан
другой круг, в который опять вписан другой правильный n - угольник
и так до бесконечности. Найти сумму площадей всех указанных n -
угольников.
Решение
Заметим, что каждый последующий
многоугольник подобен предыдущему с коэффициентом подобия 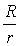 ,
где R и r – соответственно
радиусы описанной и вписанной окружностей в предыдущий многоугольник.
,
где R и r – соответственно
радиусы описанной и вписанной окружностей в предыдущий многоугольник.
Откуда, ввиду 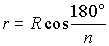 (см. формулы для правильного n - угольника), находим коэффициент
подобия
(см. формулы для правильного n - угольника), находим коэффициент
подобия 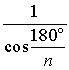 .
.
Тогда, если 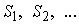 – площади первого, второго, ... многоугольников, то
– площади первого, второго, ... многоугольников, то
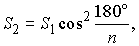
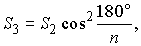 ...
Замечаем бесконечно убывающую прогрессию со знаменателем
...
Замечаем бесконечно убывающую прогрессию со знаменателем 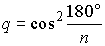 .
.
Найдем сумму членов этой прогрессии
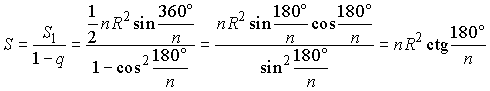 .
.
Ответ: 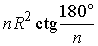 .
.
По видимому, наиболее часто встречающимся многоугольником в заданиях вступительных
экзаменов является трапеция. Сначала приведем одну известную задачу из
золотого фонда геометрии о трапеции.
Пример 6.8.6.
Доказать, что прямая, проходящая через точку пересечения продолжений боковых
сторон трапеции и через точку пересечения ее диагоналей, делит каждое основание
этой трапеции пополам.
Решение
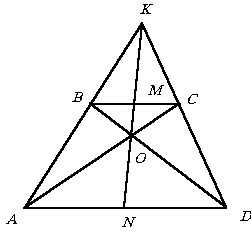 |
Положим BM = x и CM = y. Из параллельности прямых AD
и BC легко получаем подобные
треугольники. DBKM
подобен DAKN
и DCKM
подобен DDKN
с одним и тем же коэффициентом подобия 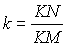 ,
т.е. AN = k ЧBM
= kx и DN = k ЧCM
= ky. ,
т.е. AN = k ЧBM
= kx и DN = k ЧCM
= ky.
Далее, DBOC
подобен DDOA
с коэффициентом подобия 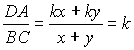 .
Но DBOM
подобен DDON
и DBOC
подобен DDOA
с одним и тем же коэффициентом подобия .
Но DBOM
подобен DDON
и DBOC
подобен DDOA
с одним и тем же коэффициентом подобия 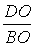 , а значит,
, а значит, 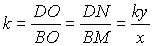 . . |
Из равенства 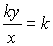 имеем x = y, а значит, BM = CM и AN = DN. Что и требовалось
доказать.
имеем x = y, а значит, BM = CM и AN = DN. Что и требовалось
доказать.
@
При решении задач на трапецию, в которых идет речь об ее диагоналях, иногда
помогает следующее дополнительное построение.
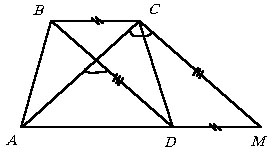 |
Достроим к трапеции ABCD параллелограмм BCMD (см. рисунок). Тогда треугольник
ACM имеет боковые стороны, равные диагоналям трапеции; основание, равное
сумме оснований трапеции; угол при вершине, равный углу между диагоналями
трапеции; площадь, равную площади трапеции. |
Попробуйте
самостоятельно объяснить эти утверждения.
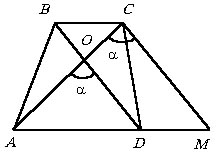
Пример 6.8.7.
Один из углов между диагоналями трапеции равен 120°.
Найти площадь трапеции, если одна из ее диагоналей равна 14 см,
а средняя линия 13 см.
Решение
Положим MC = x и по теореме косинусов в треугольнике ACM
получим 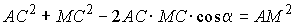 , а значит,
, а значит,
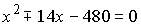 и
и 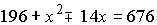 .
.
Дискриминант уравнения равен 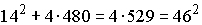 ,
откуда находим
,
откуда находим 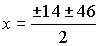 .
Так как x > 0, то
.
Так как x > 0, то 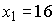 и
и 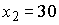 (MC = 16 соответствует a
= 120°
и MC = 30 соответствует a
= 60°).
(MC = 16 соответствует a
= 120°
и MC = 30 соответствует a
= 60°).
Учитывая, что 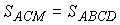 ,
находим
,
находим
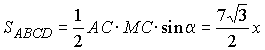 ,
т.е. либо
,
т.е. либо 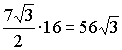 (см
(см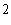 ),
либо
),
либо 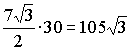 (см
(см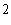 ).
).
Ответ: 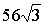 см
см или
или 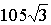 см
см .
.
ВПЕРЕД
| НАЗАД | ГЛАВНАЯ
| ПЛАНИМЕТРИЯ | СТЕРЕОМЕТРИЯ


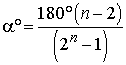 .
.
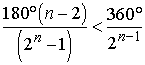 ,
которое после преобразований принимает вид
,
которое после преобразований принимает вид


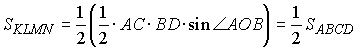 ,
,
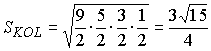 ,
и поэтому
,
и поэтому 





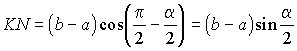 .
.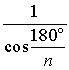 .
.
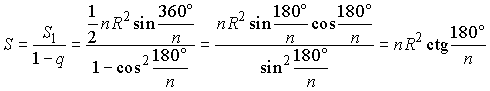 .
.

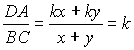 .
Но DBOM
подобен DDON
и DBOC
подобен DDOA
с одним и тем же коэффициентом подобия
.
Но DBOM
подобен DDON
и DBOC
подобен DDOA
с одним и тем же коэффициентом подобия 
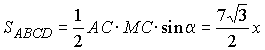 ,
т.е. либо
,
т.е. либо 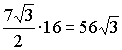 (см
(см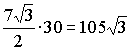 (см
(см