6.6.1. В треугольнике ABC на стороне AC выбрана точка M, равноудаленная от прямых AB и BC. Найти AM, если AB = 4, BC = 5 и AC = 6.

       Ответ: .

       6.6.2. В треугольнике ABC точка M является серединой стороны AC. Найти BM, если AB = 24, BC = 10 и AC = 26.

       Ответ: 13.

      6.6.3. Окружность с центром O вписана в угол с вершиной B. Точки A и C лежат на сторонах угла так, что точка O принадлежит отрезку AC. Найти AO, если AB = 7, BC = 8  и AC = 9.

     Ответ: 4,2.

     6.6.4. В треугольнике ABC точка M является точкой касания вписанной окружности со стороной AC. Найти AM, если AB = 6, BC = 8 и AC = 10.

     Ответ: 4.

     6.6.5. В треугольнике ABC точка M является основанием высоты, проведенной из вершины B. Найти AM, если AB = 25, BC = 40 и AC = 39.

     Ответ: 7.

     6.6.6. Внутри треугольника ABC выбрана точка M, равноудаленная от его вершин. Найти AC, если AB = BC =  и AM = 1.

     Ответ: .

     6.6.7. Внутри треугольника ABC выбрана точка M, равноудаленная от его сторон. Найти AM, если AB = 5, BC = 12  и AC = 13.

     Ответ: .
     6.6.8. В треугольнике ABC известны AB = 4, AC = 5 и 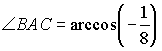. Найти расстояние от точки B до середины отрезка AC.

     Ответ: 3.

     6.6.9. Найти радиус описанной окружности около треугольника ABC, если BC = 8 и отношение высоты из вершины C  к стороне AC равно 4/5.

     Ответ: 5.

    6.6.10. В треугольнике ABC известно AC = 4, BC = 3 и . Найти отношение высоты к медиане, проведенных из вершины A.

    Ответ: 1.

    6.6.11. В треугольнике взяли две произвольные точки. Доказать, что расстояние между ними не превышает большей стороны треугольника.

    6.6.12. В плоскости расположены четыре точки A, B, C, D. Длины отрезков AB, BC, DA и AC записали в порядке возрастания и получили 3 см, 5 см, 7 см, 13 см и 19 см. Найти AC.

    Ответ: 7 см.

    6.6.13. Точка O лежит внутри треугольника ABC с периметром P. Доказать, что

    6.6.14. В треугольнике ABC взяли три точки M, P и H так, что P лежит на стороне AB и отрезки AM, MP, PH  и HB составляют ломаную без самопересечений. Доказать, что
РAMP + РPHB = РACB + РCAM + РMPH + РHBC.

    6.6.15. В треугольнике ABC медиана t = 1 и высота BH  пересекаются в точке K (точки M и H) лежат соответственно на сторонах BC и AC. Найти AC, если BC = 8 см, AK = 2 см, KM = 3 см.

    Ответ: 6 см.

    6.6.16. В плоскости выбрана точка M, равноудаленная от вершин треугольника ABC, лежащего в этой же плоскости. Найти сторону треугольника AC, если AB = 3, BC = 4 и AM = 2.5.

    Ответ: 5 или 1,4.

    6.6.17. Найти длины сторон AB и AC треугольника ABC, если длины высот треугольника, проведенных из вершин A и B, соответственно равны 1 см и 8/5 см, а сторона BC равна 2 см.

Ответ:  см, а 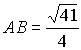 см или  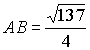см.

    6.6.18. В треугольнике ABC точки M и L – основания высот, проведенных соответственно из вершин B и C, а точки M и N – середины сторон AC и AB соответственно. Найти угол A, если известно, что прямые ML и KN параллельны.

    Ответ: РA = 60° или РA = 120° .

    6.6.19. В равнобедренном треугольнике с боковой стороной 1 и углом при вершине 36°  провели две разные по длине биссектрисы. Используя этот рисунок, доказать, что .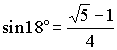

    6.6.20. В треугольнике ABC точка M делит отрезок AB в отношении 4 : 3, а точка P делит отрезок BC в отношении 2 : 3. Отрезки AP и CM пересекаются в точке O. Найти площадь треугольника ABC, если известно, что площади треугольников AOM и COP соответственно равны 9 и 10 см.

    Ответ: 35 см.

    6.6.21. В треугольнике одна из высот равна среднему арифметическому двух других высот, а одна из сторон вдвое больше другой стороны. Найти наибольший угол треугольника.

    Ответ: .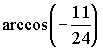

    6.6.22. Точки A,B и C являются центрами трех попарно касающихся внешним образом окружностей, причем AB = 5 см, AC = 6 см и РBAC = arccos 0,2. Найти радиусы этих трех окружностей.

    Ответ: 2 см, 3 см и 4 см.

    6.6.23. Окружность радиуса 6 см вписана в прямой угол треугольника с гипотенузой 35 см так, что центр окружности лежит на гипотенузе. Найти площадь треугольника.

    Ответ: 294 см.

    6.6.24. Периметр прямоугольного треугольника равен 12d , а площадь 6. Найти длину описанной около треугольника окружности.

    Ответ: 5 pd .

    6.6.25. В треугольнике ABC стороны AB и BC соответственно равны 5 и 4 см. Найти сторону AC, если известно, что центр вписанной в треугольник ABC окружности делит биссектрису угла C, считая от вершины, в отношении 2 : 1.

    Ответ: 6 см.

    6.6.26. В прямоугольный треугольник ABC вписана окружность и около него описана окружность. Расстояние между центрами этих окружностей вдвое больше радиуса вписанной окружности. Найти углы треугольника.

    Ответ: .
 
    6.6.27. На окружности радиуса 12 см с центром в точке O лежат точки A и B. Прямые AC и BC касаются этой окружности. Другая окружность с центром в точке M вписана в треугольник ABC и касается стороны AC в точке K, а стороны BC в точке P. Расстояние от точки M до прямой KP равно 3 см. Найти величину угла AOB.

    Ответ: .

    6.6.28. Основание равнобедренного треугольника равно a, угол при вершине равен a
Найти длину биссектрисы, проведенной к боковой стороне.
     Ответ: .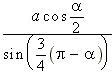
    6.6.29.  Окружность радиуса  R  касается сторон AB  и BC  треугольника ABC  в точках A и C  соответственно и пересекает медиану BD  в точке L  так, что . Найти площадь треугольника.
    Ответ: .
    6.6.30. В равнобедренном треугольнике угол между высотой, проведенной к боковой стороне, и основанием равен a, радиус вписанной окружности равен r . Найти площадь треугольника.
    Ответ: .
    6.6.31. Найти отношение радиусов вписанного и описанного кругов для равнобедренного треугольника с углом a  при основании.
    Ответ: .
    6.6.32. Угол при основании равнобедренного треугольника равен a (a > 45° ), а площадь равна  S. Найти площадь треугольника, вершинами которого служат основания высот треугольника  ABC.
    Ответ: .
    6.6.33.  В треугольнике ABC  сторона AB = 2 см, BC = 3  см, угол ABC = 60° . Найти площадь треугольника, образованного высотой и медианой треугольника  ABC, проведенных из вершины  B.
    Ответ:  см .
    6.6.34.  Равнобочная трапеция, у которой угол при основании равен 60°  описана около окружности. В каком отношении прямая, соединяющая точки касания окружности с боковыми сторонами, делит площадь трапеции.
    Ответ: .