@ Наиболее употребимой формулой, связывающей площадь, сторону и высоту на эту сторону, является . Эта формула замечательна тем, что компоненты a  и , S и a или S и  определяют треугольник неоднозначно, но, тем не менее, можно найти недостающую третью из этих компонент. Необходимо представлять себе расположение высот треугольника в зависимости от его вида: если он остроугольный, то все три высоты внутри него; если он прямоугольный, то одна высота внутри него, а две другие совпадают с катетами; если он тупоугольный, то одна высота внутри него, а две другие, опущенные из острых углов, вне его. Известно, что прямые, содержащие высоты треугольника, пересекаются в одной точке, называемой ортоцентром треугольника (такое название точки связано с тем, что она служит центром вписанной окружности в треугольник, вершины которого являются основаниями высот данного остроугольного треугольника).

Пример 6.3.1.

      а) Доказать, что в любом треугольнике ABC, для любой точки D стороны BC (D не совпадает с B и C) имеет место равенство

;

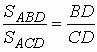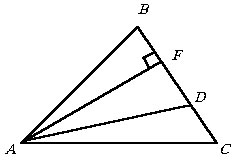
      б) Доказать, что в любом равностороннем треугольнике ABC  сумма расстояний от всякой внутренней точки треугольника до его сторон равна высоте треугольника.  

      Утверждения а) и б) примера 6.3.1. имеют довольно частое применение при решении заданий вступительных экзаменов, поэтому приведем их краткие доказательства.
 
 

а)	Пусть AF – высота треугольника ABC, проведенная из вершины A. Тогда AF является высотой для треугольника ABD и для треугольника ACD. Поэтому  и   .

      Разделив почленно обе части этих равенств, получим требуемое соотношение.

      б) Полезно знать, что для построения в тетради равностороннего треугольника используют тот факт, что равнобедренный треугольник с основанием 8 и высотой 7 имеет боковые стороны .
 

Пусть O – внутренняя точка треугольника ABC и D, E, F – основания перпендикуляров из нее на стороны треугольника. Тогда      , т.е.  (в ходе преобразований учли, что AB = BC = AC).

      Теперь попытайтесь самостоятельно доказать, что в любом правильном n - угольнике (n і3) сумма расстояний от любой его внутренней точки до прямых, проходящих через его стороны, есть величина постоянная, равная n Чr, где r – радиус вписанной в данный n - угольник окружности.

Пример 6.3.2. (КубГУ, эконом., 1987 г.)

      В равнобедренном прямоугольном треугольнике длина катета равна 1. Прямая, проходящая через вершину острого угла, делит площадь треугольника в отношении 1 : 4. Найти длину отрезка прямой, лежащего внутри треугольника.

Указание: воспользуйтесь рассуждениями в ходе доказательства утверждения примера 6.3.1 а) и учтите две возможности прохождения прямой, делящей площадь треугольника в заданном отношении.

Ответ:  или .

@ Для нахождения площади треугольника часто используют еще две формулы:
 

; (1)   , (2)  где p – полупериметр треугольника (формула Герона) и a, b, c – его стороны.

Пример 6.3.3.

      В треугольнике ABC сторона AB = 7  см, AC = 8 см, BC = 9 см. Найти площадь треугольника, образованного высотой и медианой треугольника ABC, проведенных из вершины B.

Эта задача имеет много вариантов решений. Для иллюстрации формул (1) и (2) предлагаем следующий (нелучший) вариант.

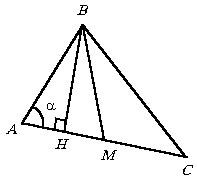Основания высоты и медианы обозначим соответственно через H и M, положим РA = a.   Так как , то по формуле Герона . Точка M делит отрезок AC пополам и поэтому , т.е. .

С другой стороны, , откуда получаем  и .

Поэтому , а значит .

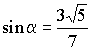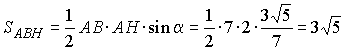Так как , то окончательно  (см).

Ответ:  см.

Теперь отметим одно очень важное свойство площадей подобных фигур: если фигура  подобна фигуре  с коэффициентом подобия k, то отношение площадей фигур  и  равно .

 Применим это свойство для решения следующего задания.

Пример 6.3.4. (КубГУ, эконом., 1988 г.)

     В треугольнике ABC  проведены медианы AM и BK и высота CN. Найти отношение площадей треугольников ABC и MNK.

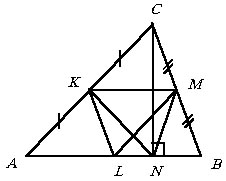Изображать медианы AM и BK не будем. В середине стороны AB отметим точку L. Тогда KM, ML, KL – средние линии в треугольнике ABC. Поэтому KM ззAB, KL ззBC  и ML ззAC, а значит треугольники MKL и ABC подобны с коэффициентом подобия k = 2 (учли, что ).  Поэтому .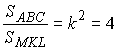

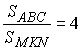     Поэтому , и окончательно находим .

Ответ: 4.

     Замечание. Из равновеликости треугольников MKL и MKN легко сделать заключение, что площадь любого треугольника, у которого две вершины в точках M и K, а третья на стороне AB, будет равна площади треугольника MKL. Поэтому несущественно, что проведено из вершины C – биссектриса, медиана, выстота или произвольная прямая, пересекающая сторону AB.

@ Отметим, что высоты треугольника обратно пропорциональны сторонам, на которые они опущены, так как ,  и . Поэтому отрезки, длины которых равны x,y и z, могут служить высотами некоторого треугольника тогда и только тогда, когда сумма меньших чисел из набора ,  и  больше большего числа. Вообще, когда речь идет о высотах треугольника, следует рассматривать его площадь, что в большинстве задач приводит к их решению.

 
Пример 6.3.5. (КубГУ, матем., 1994 г.)

     Найти площадь равнобедренного треугольника, если высота, опущенная на основание, равна 10, а опущенная на боковую сторону равна 12.

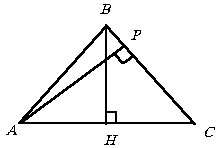P и H – основания высот, опущенных соответственно из вершин A и B равнобедренного треугольника ABC (AB = BC ). По условию AP = 12 и BH = 10. Пусть BC = y и CH = x.   Тогда AC = 2x и , т.е. 6y = 10x  и .

      По теореме Пифагора из треугольника BHC имеем , а значит  и .

     Поэтому  (ед).

Ответ: 75 ед.