Известно, что все три медианы треугольника пересекаются в одной точке, причем эта точка делит каждую из них в отношении 2 : 1, считая от вершины.

Пример 6.4.1. (КубГУ, матем., 1979 г.)

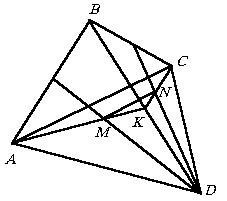
В выпуклом четырехугольнике ABCD расстояние между точками пересечения медиан треугольников ABD и BCD равно a. Определить AC.

Пусть M и N – точки пересечения медиан в треугольниках ABD и BCD соответственно и K – середина отрезка BD. Тогда , и по первому признаку треугольники AKC и MKN подобны с коэффициентом подобия . Поэтому AC = 3 MN = 3 a.

       Для нахождения медианы треугольника по трем его сторонам удобно использовать рассуждения при решении типовой задачи из примера 6.2.7 а).

@
 

,   ,   .

Пример 6.4.2.

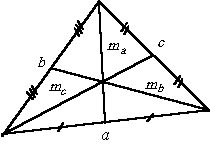
      Определить стороны треугольника, если его медианы равны   и .

      Полагая в предыдущих трех равенствах ,  и , после возведения обеих частей в квадрат получим

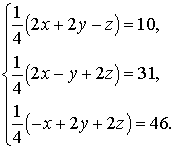
      Решая систему линейных уравнений, найдем x = 16, y = 36 и z = 64, а значит стороны треугольника равны 4; 6 и 8.

Ответ: 4; 6 и 8 .
@При решении задач, в которых упоминается медиана треугольника, часто достраивают треугольник до параллелограмма так, чтобы медиана была половиной диагонали.
 

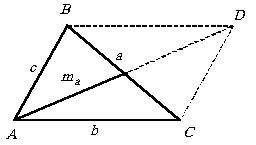Так как в параллелограмме сумма квадратов всех его сторон равна сумме квадратов диагоналей, то , и опять получаем выражение медианы через стороны треугольника:  .

Пример 6.4.3.

      Доказать, что три данных отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.

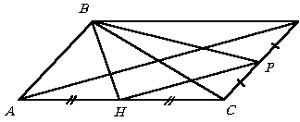
     Указание: при выполнении этого задания следует учесть, что для любого треугольника ABC можно составить треугольник BHP из его медиан как указано на рисунке, а по треугольнику из медиан BHP можно восстановить треугольник ABC.

Пример 6.4.4. (КубГУ, матем., 1986 г.)

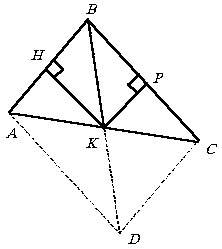
      Длина медианы BK остроугольного треугольника ABC равна 8 см. Длины ортогональных проекций этой медианы на стороны AB  и BC равны 6 см и  см соответственно. Найти длину стороны AC.

Пусть AK = BK = x (см. рисунок).

По теореме Пифагора имеем

и ,

а значит  и .
 

Так как сумма квадратов диагоналей параллелограмма ABCD равна сумме квадратов всех его сторон, то получаем уравнение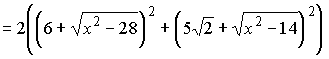  .  После преобразований имеем  . Для удобства, полагая , получаем  или .

       После преобразований получаем , и поэтому t = 1.
      Откуда находим  и .
      Поэтому  (см).
      Ответ:  см.

@Перейдем к рассмотрению биссектрис треугольника. Известно, что все биссектрисы внутренних углов треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник. Имеет место следующая теорема.
 

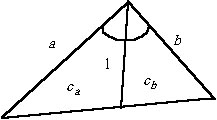Теорема о биссектрисе        Основание биссектрисы внутреннего угла треугольника делит его сторону на части, пропорциональные прилежащим сторонам, т.е. согласно имеющемуся рисунку  .

      Удобно теорему формулировать так:

      а) существует t такое, что  и ;

     б) существует k такое, что  и .

     Докажите эту теорему, используя теорему синусов.

Пример 6.4.5.

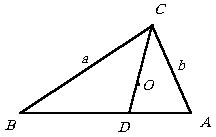
      Найти биссектрису угла B треугольника ABC и определить, в каком отношении центр вписанной в треугольник окружности делит эту биссектрису, если AB = 4, BC = 5 и AC = 6.

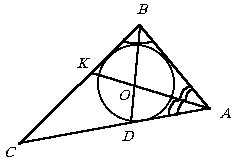Пусть BD и AK – биссектрисы углов B и A треугольника ABC и O – центр вписанной окружности.        Так как AB = 4 и BC = 5, то по теореме о биссектрисе AD = 4t и CD = 5t, поэтому AC = 6 = 4t + 5t, т.е. 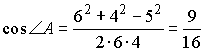, и тогда .

  и

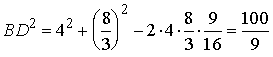, т.е. .

      И, наконец, определим по теореме о биссектрисе из треугольника BAD, в каком отношении точка O делит отрезок BD:

.

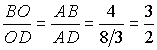Ответ:  и .

@Полезной и легко запоминаемой является формула

,

а также отношения, которые позволяют установить, как точка пересечения биссектрис делит биссектрису .  .

      Биссектриса угла, меньшего 180°, – это геометрическое место точек, равноудаленных от сторон этого угла, а также это геометрическое место точек – центров окружностей, вписанных в этот угол.

Пример 6.4.6.
      В треугольнике ABC известно, что AB = 4, BC = 5 и . Центр O окружности, вписанной в угол B, лежит на стороне AC. Найти BO.

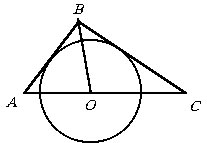Ясно, что BO – биссектриса угла B.  По теореме косинусов находим   , т.е. AC = 6.  Далее, как и в примере 6.4.5. находим .

      Ответ: .

Пример 6.4.7. (КубГУ, физич., 1975 г.)

       Найти биссектрисы острых углов в прямоугольном треугольнике, катеты которого равны 6 и 8 см.

Пусть ABC – прямоугольный треугольник, у которого AB = 6, BC = 8, РB = 90 °, P и H – основания биссектрис углов C и A соответственно. Тогда по теореме Пифагора .  По теореме о биссектрисе BP = 8t и Pa = 10t , откуда AB = AB = 6 = 8t + 10t и .        Поэтому 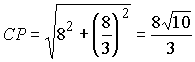, и по теореме Пифагора . Аналогично находим .

Ответ:  см,  см.