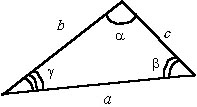
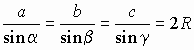 ,
,
где R – радиус описанной около треугольника окружности.
![]() ,
т.е.
,
т.е.
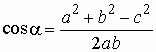 .
.
Будем говорить, что данные компоненты (стороны, углы и др.) определяют фигуру однозначно, если другая фигура с такими же компонентами обязательно равна исходной. Например, для треугольника две стороны и угол между ними, сторона и два прилежащих к ней угла или три стороны по признакам равенства треугольников определяют всякий треугольник однозначно. Возможны и другие случаи однозначного определения треугольника: равнобедренный треугольник с данными основанием и опущенной на него высотой, треугольник с данными тремя медианами, треугольник с данными тремя высотами и т.п. Очень важно при решении планиметрической задачи определить однозначно фигуру и далее найти те ее неизвестные компоненты, которые необходимы для продолжения хода решения задачи.
Для нахождения неизвестных сторон и углов однозначно определенного треугольника
обычно используют теоремы синусов и косинусов.
@
 |
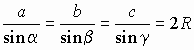 , ,
где R – радиус описанной около треугольника окружности.
|

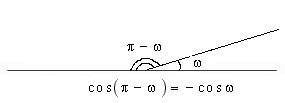 .
.Следующий пример иллюстрирует применение теоремы синусов и косинусов для нахождения неизвестных сторон и углов некоторых однозначно определенных треугольников. Выполнить самостоятельно.
Пример 6.2.1.
а)
 |
Дано: a, b, c.
Найти: a, b, g. |
Дано: a, b, g.
Найти: c, a, b. |
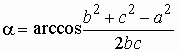 ,
, 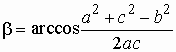 ,
g = p - a - b;
,
g = p - a - b;
б) ![]() ,
, 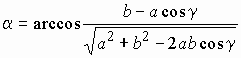 ,
b = p - g - a;
,
b = p - g - a;
в) a
= p - b - g, 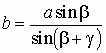 ,
, 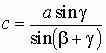 .
.
@ Как правило, при решении треугольников сначала стремятся определить три стороны, а затем находят необходимые компоненты. При известных трех сторонах треугольника для более точного изображения эскиза чертежа необходимо уметь определять вид треугольника (остроугольный, прямоугольный или тупоугольный).
Из формулы, следующей из теоремы косинусов, примененной к наибольшему углу, учитывая знак косинуса, можно получить соотношения между квадратами сторон, позволяющие определить вид треугольника.
Если cos a
< 0,
то ![]() , т.е.
, т.е. ![]() ,
,
если cos a
> 0,
то ![]() , т.е.
, т.е. ![]() ,
,
если cos a
= 0,
то ![]() , т.е.
, т.е. ![]() .
.
Следовательно,
треугольник, у которого c – наибольшая сторона, будет тупоугольный, если ![]() ;
остроугольный, если
;
остроугольный, если ![]() , и
прямоугольный, если
, и
прямоугольный, если ![]() .
.
Упражнение 6.2.2.
По длинам трех сторон определить вид треугольника:
а) 5; 3; 4 ; б) 12; 5; 13 ; в) 3; 2; 4 ; г) 7; 8; 6 ; д) 7; 2; 3.
Указание: известно, что против большей стороны в треугольнике лежит больший угол, и обратно. Косинус большего угла можно найти по формуле, следующей из теоремы косинусов.
Ответ: а) и б) прямоугольные, в) тупоугольный, г) остроугольный,
д) не существует.
В связи с упражнением 6.2.2. д) следует отметить довольно часто применяемое при решении геометрических задач так называемое неравенство треугольника: @ из трех отрезков можно составить треугольник тогда и только тогда, когда сумма длин меньших из них больше длины большего.
Ещё используется другой вариант формулировки неравенства треугольника: для любых трех точек A, B и C имеем чAB-BCчЈ AC Ј AB+BC ; причем правое неравенство обращается в равенство лишь в случае, когда точка B лежит на отрезке AC; а левое неравенство обращается в равенство лишь в случае, когда точки A,B и C лежат на одной прямой и точка B не лежит внутри отрезка AC.
Теперь приведем примеры решения некоторых заданий вступительных экзаменов в КубГУ.
Пример 6.2.3. (КубГУ, матем., 1993 г.)
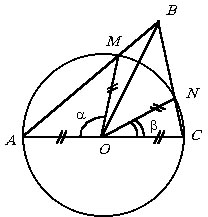
На основании AC треугольника ABC, как на диаметре построена окружность, которая пересекает стороны AB и BC в точках M и N соответственно. Найти радиус окружности, если AB = a, ИAM = a, ИCN = b.
Из равнобедренного треугольника
AOM находим РA
= (p - a)
/ 2, а из равнобедренного треугольника
CON находим РС
= (p - b)
/ 2, поэтому РB
= p - РA
- РС
= (a +
b) / 2.
 |
Смысл нахождения углов A и B заключается в том, что в треугольнике
ABC мы будем знать сторону AB = a и два прилежащих
к ней угла, т.е. DABC
определен однозначно. Осталось
найти неизвестную сторону AC как
и в примере 6.2.1 в):
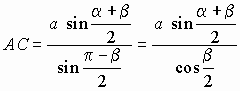 . .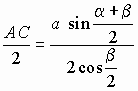 . . |
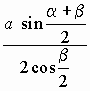 .
.
Пример 6.2.4. (КубГУ, матем., 1979 г.)
В треугольник ABC вписана окружность. Точки D, E, F – точки касания сторон AB, BC, CA соответственно. Определить площадь треугольника ABC, если AB = a, BC = b, РDEF = 60°.
Это задание интересно тем, что DABC согласно рассуждениям ниже будет определен неоднозначно. Тем не менее, с такими компонентами может существовать не более двух различных треугольников!
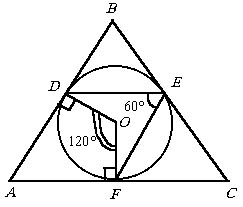 |
Пусть O
– центр вписанной окружности. Так как вписанный угол DEF равен 60°,
то центральный угол DOF равен 120°. Сумма углов в четырехугольнике
ADOF равна 360°. Итак, мы о треугольнике ABC знаем
его две стороны AB = a, BC = b, а также угол A (не между
ними!).
Далее стремимся найти третью сторону AC. Полагая AC = x, по теореме косинусов имеем 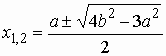 .
Тогда площадь треугольника ABC находим по формуле .
Тогда площадь треугольника ABC находим по формуле 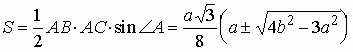 . .
Ответ неоднозначен! |
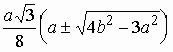 .
.
Замечание. Желательно при решении предыдущей задачи не ограничиваться указанным ответом.
Так, если 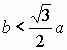 ,
(т.е.
,
(т.е. ![]() ),
то задача вообще не имеет решения.
),
то задача вообще не имеет решения.
Если же 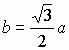 или b > a, (т.е.
или b > a, (т.е. ![]() или
или ![]() ),
то задача имеет единственное решение:
),
то задача имеет единственное решение: 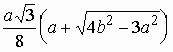 .
.
И только лишь в случае, когда 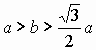 (т.е.
(т.е. ![]() ),
мы получаем ранее указанный двузначный ответ.
),
мы получаем ранее указанный двузначный ответ.
Теперь для иллюстрации применения неравенства треугольника приведем решение
одного несложного задания устных экзаменов на математический факультет
КубГУ.
Пример 6.2.5.
Доказать, что сумма двух медиан треугольника меньше его периметра.
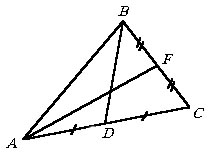 |
По неравенству треугольника из DABF
и DACF
имеем AF < AB + BF и AF < AC + CF, т.е.
2AF < AB + BF + AC + CF
= Откуда, аналогично из DABD
и DCBD,
получим 2 BD < |
Доказать, что в любом треугольнике ABC для любой точки D, лежащей внутри него или на его стороне, длина отрезка AD меньше полупериметра треугольника ABC.
Указание: используйте рассуждения, подобные приведенным в начале доказательства предыдущего задания.
В заключение этого параграфа приведем три типовые задачи, в решении которых главную роль играет теорема косинусов.
Пример 6.2.7.
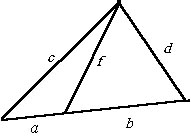
Для иллюстрации решим а). |
а) Дано: a, b, c, d .
Найти f.
б) Дано: a, b, c, f . Найти d. в) Дано: a, c, d, f. Найти b. |
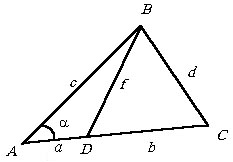 |
Введем дополнительно РA
= a. Из
DABC
находим
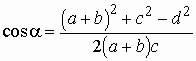 . .
Тогда из DABD находим т.е. 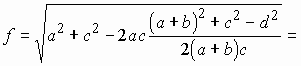 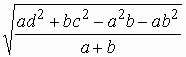 . . |