 |
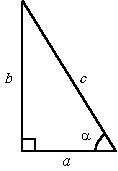
В прямоугольном
треугольнике сторона, лежащая против прямого угла, называется гипотенузой,
а две другие стороны – катетами. Известна теорема Пифагора: квадрат гипотенузы
равен сумме квадратов катетов, т.е. |
Используя прямоугольный треугольник и необходимые преобразования, доказать равенства:
| 1) |
2) |
| 3) |
4) |
| 5) |
6) |
а)
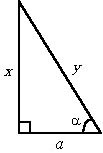 |
Дано: a, a.
Найти: x, y. |
б)
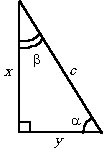 |
Дано: c, a.
Найти: b, x, y. |
в)
 |
Дано: a, b .
Найти: x, a. |
г)
 |
Дано: a, c .
Найти: x, a. |
в) ![]() ,
, ![]() ;
г)
;
г) ![]() ,
, ![]() .
.
Необходимо научиться свободно связывать соотношениями стороны и углы прямоугольного треугольника с использованием тригонометрических и обратных тригонометрических функций.
Приведем примеры решения двух заданий вступительного экзамена.
Пример 6.1.2. (КубГУ, матем., 1994 г.)
Вычислить катеты прямоугольного треугольника, зная длину c его гипотенузы и длину 1 биссектрисы одного из острых углов.
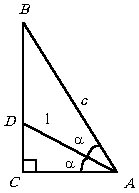 |
Полагаем РA=2
a. Из
DADC
имеем AC = 1Чcos
a, а
из DABC
- AC = c Чcos
2 a.
Учитывая Откуда 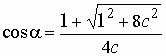 и поэтому и поэтому |
Пример 6.1.3. (КубГУ, матем., предварит. экз., 1994 г.)
Периметр прямоугольного треугольника ABC равен 10 . Из вершины прямого угла B на гипотенузу опущена высота BD. Периметр треугольника ABD равен 6. Найти величину угла A.
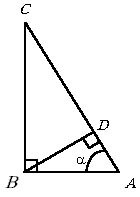 |
Положим РA= a.
Из DABC
имеем AB = AC Чcos
a и
BC = AC Чsin
a, откуда
периметр DABC
равен AC +
AC Чcos
a + AC
Чsin
a, т.е.
AC Ч(1+
cos a +
sin a)
=10.
Из DABD имеем AD = AB Чcos a и BD = AB Чsin a, а значит периметр DABD равен AB + AB Чcos a + AB Чsin a,т.е. AB Ч(1+ cos a + sin a) =6. Таким образом, 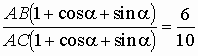 и
и |