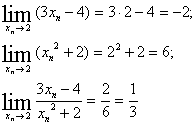на главную страницу

Какое из положений теории относятся к приведенным ниже заданиям. Укажите соответствие заданий и решений. Ответы занесите в таблицу.

Задания	Решения
А Дана функция f(x)=x^2и x0=1. Вблизи точки x0 положим x=1+h, где h-переменная, принимающая сколь угодно малые значения. Учитывая это, найдите приближение функции x^2 линейной на малом интервале.	А1 С 1000001-го номера
Б Почему в примере А при переходе к приближенному равенству отбросили h^2?	Б1 Пусть xn– некоторая последовательность значений переменной x сходящаяся к числу 2, тогда n-й член соответствующей последовательности значений функции имеет вид . Полученный результат справедлив для любой последовательности yn, сходящейся к числу 2, значит, по определению
В Чем является прямая y=2x-1 по отношению к функции y=x^2 в окрестности точки x0=1?	В1 Исчезающая (бесконечно малая) величина
Г Дана последовательность 1, 1/2, 1/3,…1/n,… С какого номера ее члены становятся меньше 10^-6 ?	Г1 Бесконечно малая величина.
Д Как называется переменная X указанной последовательности?	Д1 (1+h)^2=1+2h+h^2»1+2h=1+2(x-1)=2x-1.
Е Если x®a, то какой величиной является разность (x-a)?	Е1 h^2 уменьшается существенно быстрее, чем h, т.к. , т.е. h^2 во столько же раз меньше |h|, во сколько |h| меньше 1.
Ж Опираясь на определения предела, выясните чему равен предел функции при x®2.	Ж1 Прямая y=2x-1 в точке M(1;1) примыкает к графику функции y=x^2 более тесно, чем любая другая прямая, проходящая через эту точку. Значит, эта прямая – это касательная к графику в данной точке.
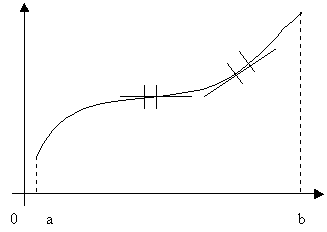
З Найдите, если известно, что функция f(x) непрерывна в т. x0=2.	З1 Пусть функция возрастает на некотором интервале. Тогда ее график представляет собой линию, поднимающуюся при движении слева направо. Поэтому маленький отрезок касательной , почти совпадающий с кусочком графика, примыкающим к точке касания, будет тоже поднимающимся или, в крайнем случае, будет горизонтальным отрезком. Следовательно, угловой коэффициент касательной в любой точке кривой (т.е. значение производной) больше или равен нулю.
И Каким будет угловой коэффициент касательной в любой точке возрастающей функции.	И1 (x^4)¢=4x^3; (x^4)²=12x^2; (x^4)¢²=24x; (x^4)^(4)=24: (x^4)^(n)=0 при n5
К Найти производные всех порядков от функции x^4	К1 Если известно, что функция f(x) непрерывна в точке x0, то вычисление предела сводится к простому вычислению значения функции в этой точке. Значит искомый предел равен значению функции в точке x=2 , т. е.