ТЕОРИЯ

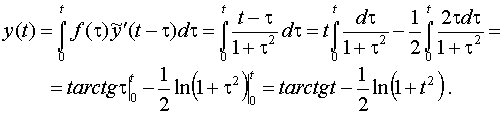
Возникли трудности? Посмотри приведенное ниже решение.

Задание 32.

а)Найти операционным методом частное решение дифференциального уравнения ,

удовлетворяющее начальным условиям у(0)=0, у¢(0)=0.

Решение.

Пусть y(t)=Y(p). .

Тогда по свойству дифференцирования оригинала с учетом начальных условий имеем

.

По таблице .

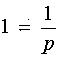Переходя в исходном дифференциальном уравнении к изображениям, получим соответствующее операторное уравнение

,

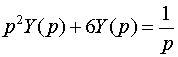из которого находим

.

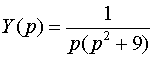Разлагая эту дробь на элементарные, получим

.

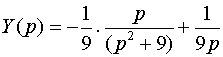Пользуясь таблицей, находим решение:

.

Задание 32.

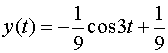б) Найти операционным методом частное решение дифференциального уравнения

,

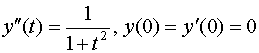удовлетворяющее начальным условиям у(0)=0, у¢(0)=0.

Решение.

Составим вспомогательное уравнение

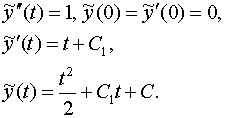
Воспользуемся начальными условиями:

,

.

Итак,

.

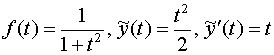Тогда