
Задание
18.
Найти все особые точки функции в плоскости ![]() и
выяснить их характер
и
выяснить их характер
а) 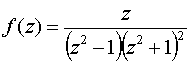 ;
б)
;
б) ![]() ; в)
; в) 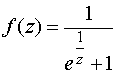 ;
;
Решение:
а) Функцию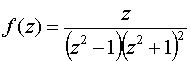
можно представить в виде
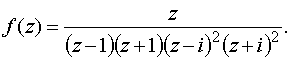
Воспользовавшись теперь сделанным выше замечанием, имеем: ± 1 – полюсы первого порядка (простые полюсы); ± i – полюсы второго порядка.
б) Докажем, что точка z=0 является существенно особой точкой .
Функция
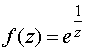 регулярна в кольцевой области {z:
0<|z|<¥ }.
регулярна в кольцевой области {z:
0<|z|<¥ }.
Покажем,
что не существует ни конечного, ни бесконечного предела f (z)
при z® 0. Если z стремится к нулю
вдоль положительной части действительной оси, (z=x>0), то 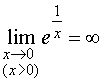 ,
однако
,
однако 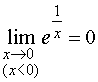 . Таким образом,
. Таким образом, 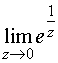 не существует, следовательно, z=0 – существенно особая точка для
не существует, следовательно, z=0 – существенно особая точка для ![]() .
Точка z=¥ является
точкой, в которой функция f (z) регулярна.
.
Точка z=¥ является
точкой, в которой функция f (z) регулярна.
в) Найдем нули знаменателя f(z), т. е. корни уравнения
![]() .
.
Из равенства
![]() следует, что знаменатель у функции
f (z) обращается в нуль в точках
следует, что знаменатель у функции
f (z) обращается в нуль в точках 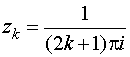 ,
k=0, ± 1,…,
которые и будут полюсами первого порядка для f (z).
Точка z=0 – не изолированная особая точка, ибо она является предельной
для полюсов. z=¥
– точка, в которой функция f (z) регулярна.
,
k=0, ± 1,…,
которые и будут полюсами первого порядка для f (z).
Точка z=0 – не изолированная особая точка, ибо она является предельной
для полюсов. z=¥
– точка, в которой функция f (z) регулярна.
Приведем еще несколько примеров исследования особых точек
Пример 1. Исследовать характер бесконечно удаленной точки для следующих функций:
а) 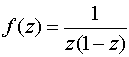 ; б)
; б)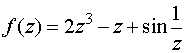 .
.
Решение.
а) Производя замену ![]() , получим
соотношение
, получим
соотношение
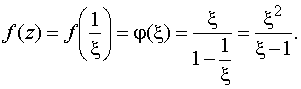
Раскладывая полученную функцию в ряд по степеням x , найдем, что при |x |<1 справедливо представление
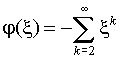 ,
,
и, следовательно,
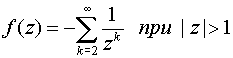 ,
,
из которого заключаем, что точка z=¥ для функции f (z) является правильной точкой.
б) Область {z: 0<|z|<¥ } является окрестностью точки z=¥ для функции f (z).
Разложим в этой области данную функцию в ряд Лорана по степеням z:
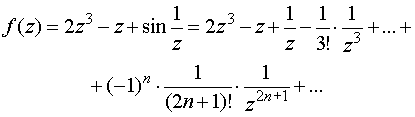
Таким образом, точка z=¥ является полюсом третьего порядка.
Пример
2. Исследовать характер особой точки z=0 для функции 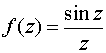 .
.
Решение. Разложим эту функцию в ряд Лорана в окрестности точки z=0. Так как
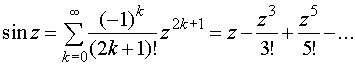 ,
,
то
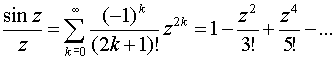 .
.
В этом
разложении главная часть отсутствует, следовательно, точка z=0 является
устранимой особой точкой функции 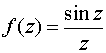 .
.
