Арифметические и геометрические прогрессии

 

1. Если сумма первого и четвертого членов арифметической прогрессии равна 14, а ее второй член меньше пятого на 6, то сумма третьего и пятого членов прогрессии равна :

1) 19 2) 20 3) 214) 22  5) 23 введите номер правильного ответа и нажмите кнопку 'проверить'

2. Если сумма первых десяти членов арифметической прогрессии равна 300, а четвертый член равен 21, то сумма третьего и шестова членов прогрессии равна:

1) 44 2) 45 3) 46 4) 47 5) 48

 

3. Если второй член геометрической прогрессии равен -6, апятый равен 48, то сумма первых шести членов прогрессии равна:

1) -63 2) 63 3) 21 4) -19 5) -72  

 

4. Если сумма первого и мятого членов геометрической прогрессии равна 820, а знаменатель равен 3, то сумма первых шести членов прогрессии равна:

1) 1820 2) 910 3) 7280 4) 3640 5) 5460

 

5. Если сумма шести первых членов геометрической прогрессии равна 910, а знаменатель равен 3, то сумма первого и пятого ее членов равна:

1) 305 2) 410 3) 205 4) 284 5) 192

 

6. Если первый член геометрической прогрессии равен 4, а четвертый член равен -32, то сумма первых ее шести членов равна:

1) 84 2) -84 3) -82 4) -6 5) 6

 

7. Если x0 - корень уравнения 1 + 3 + 5 + 7 + ... + х = 625, то значение выражения ( x0 + 1)/( x0 - 39) равно:

1) 2 2) 3 3) 4 4) 6 5) 5

 

8. Сумма всех целых чисел, кратных 7 и удовлетворяющих условию 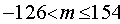, равна :

1) 630 2) 770 3) 700 4) 840 5) 707

 

9. Три числа x, y, z, образуют в указанном порядке геометрическую прогрессию с отличным от единицы знаменателем, а числа x, 2y, 3z образуют в указанном порядке арифметическую прогрессию. Тогда знаменатель геометрической прогрессии равен:       

1) 1/3 2) 1/2 3) 3 4) 2 5) 1/6

 

10. Если сумма третьего, седьмого, четырнадцатого и восемнадцатого членов арифметической прогрессии равна 10, то сумма первых двадцати членов этой прогрессии равна:

1) 40 2) 50 3) 60 4) 30 5) 45

 

11. Сумма третьего и пятого членов геометрической прогрессии равна 10, а сумма второго и четвертого членов равна 10/3. Тогда четвертый член прогрессии равен:

1) 6 2) 1/3 3) 3 4) 5 5) 4

 

12. Если второй член геометрической прогрессии равен 27, а пятый равен 1, то сумма пяти ее первых членов равна:

1) 121 2) 119 3) 108 4) 97 5) 127

 

13. Если в возрастающей геометрической прогрессии каждый член, начиная с третьего, равен сумме двух предыдущих, то ее знаменатель равен:

1) 2 2) 3/2 3) 1 + 21/2 4) (1 + 51/2)/2 5) 3

 

14. Сумма всех трехзначных натуральных чисел, кратных 23, равна:

1) 21008 2) 21528 3) 21551 4) 21028 5) 21505

 

15. Сумма всех двузначных натуральных чисел, каждое из которых при делении на 4 дает остаток, равный 3, равна:

1) 1257 2) 1261 3) 1254 4) 1269 5) 1273