квадратного трехчлена
1) координаты вершины D
являются решением системы неравенств
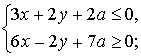
2) координаты хотя бы одной точки отрезка АС являются решением системы неравенств из пункта 1)?
| ЗАДАЧА1 | Найти
все значения параметра a, при которых
вершины двух арабол |
| ЗАДАЧА2 | При каких значениях
a график функции |
| ЗАДАЧА3 | При каком значении
a графики функций |
| ЗАДАЧА4 | Найти наименьшее
положительное значение m, при котором
функции y=ctgx и y=2sinmx
пересекаются в точке с абсциссой |
| ЗАДАЧА5 | Определить, при каком значении k
график функции |
| ЗАДАЧА6 | При каких действительных
значениях a и b
все экстремумы функции |
| ЗАДАЧА7 | При каких действительных значениях a
и b все экстремумы функции |
| ЗАДАЧА9 | Найти наибольшее значение функции |
| ЗАДАЧА10 | Для каждого отрицательного числа
a найти наименьшее значение функции |
| ЗАДАЧА11 | Найти все значения параметра a,
при каждом из которых функция |
| ЗАДАЧА12 | Найти все значения параметра a, при каждом из которых функция y=asin4x-10x+sin7x+4ax всюду убывает и не имеет критических точек. |
| ЗАДАЧА13 | При каких значениях параметра a
наименьшее значение на промежутке
квадратного трехчлена |
| ЗАДАЧА14 | При каком значении параметра a прямые, проходящие через точку M(1,1) плоскости xOy и касающиеся двух ветвей гиперболы y=a/x, (a<0) в точках А и В, образуют правильный треугольник МАВ? Найти площадь S этого треугольника. |
| ЗАДАЧА15 | Вершины А, В,
С параллелограмма АВСD имеют соответственно
координаты (–2; –3), (1; 3), (6; 1). При каких значениях параметра a:
1) координаты вершины D
являются решением системы неравенств
2) координаты хотя бы одной точки отрезка АС являются решением системы неравенств из пункта 1)? |