Неравенство ![]() равносильно совокупности систем:
равносильно совокупности систем:
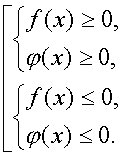
Неравенство ![]() равносильно совокупности систем
равносильно совокупности систем
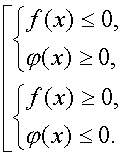
Неравенство ![]() равносильно совокупности систем:
равносильно совокупности систем:
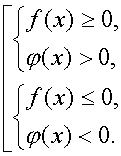
Неравенство ![]() равносильно совокупности систем:
равносильно совокупности систем:
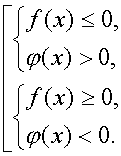
О некоторых методах решения неравенств
В этом разделе на примере некоторых типов неравенств будут рассмотрены часто встречающиеся приемы их решения.
Рекомендуем перед чтением просмотреть соответствующие темы из
справочника, приведенного в книге.При решении неравенств обычно рекомендуют рассматривать неравенство в системе с неравенствами, определяющими область определения, входящих в неравенство функций (т.е. область допустимых значений или ОДЗ), и применять метод равносильных преобразований систем.
Ключевой момент в решении неравенства – преобразование его к виду, в котором левая часть представляет собой произведение каких-либо функций, а правая – равна нулю. После такого преобразования применяют правило расщепления неравенств:
@
Правило расщепления|
Неравенство
|
Неравенство
|
|
Неравенство
|
Неравенство
|
Таким образом, при применении правила расщепления неравенств необходимо сначала аккуратно выписать все случаи, когда это неравенство справедливо, т.е. выписать совокупность соответствующих систем неравенств, а затем решить каждую из этих систем и объединить в ответе полученные множества решений.
Аналогичное правило может быть сформулировано и для строгих неравенств.
Заметим, что
при решении нестрогого неравенства в множество всех решений строгого неравенства включаются множество корней соответствующего уравнения.![]()
В процессе решения может оказаться, что в левой части (подразумевается, что правая часть равна нулю) число сомножителей бывает довольно велико, а значит, непосредственное применение правил расщепления приводит к трудоемкому решению нескольких систем. В такой ситуации, часто, оказывается эффективным применение метода интервалов.
@
Метод интервалов применяют для неравенств вида f(x)>0 (вместо знака > могут быть знакиРассмотрим важный частный случай применения метода интервалов для алгебраических неравенств.
Сформулируем
правило расстановки знаков при решении неравенств вида![]() где
где ![]() .
.
На координатную ось наносят числа
x1,x2,...,xn, которые разбивают её на интервалы знакопостоянства функции, стоящей в левой части неравенства. В промежутке справа от xn ставят знак “+”, затем, двигаясь справа налево, при переходе через точку xi меняют знак, т.е. левее xn ставят знак ”–”, затем “+” и т.д.Множество решений неравенства будет объединение интервалов, в каждом из которых поставлен знак “+”
.Аналогично может быть описано решение неравенств, в которых вместо знака
> стоят знаки <,При решении неравенств вида
![]() ;
; ![]()
правило расстановки знаков
изменяется в том смысле, что, двигаясь, справа налево, при переходе через точку xi меняют знак, если ki – нечетное, и не меняют знак, если ki четное. После этого множество решений определяют, как и в предыдущем случае.При решении рациональных неравенств
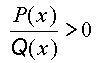 ,
,
где
P(x) и Q(x) – многочлены, методом интервалов на числовую ось наносятся точки, в которых числитель и знаменатель обращаются в ноль. Далее на полученных интервалах расставляются знаки, которые определяются или непосредственными вычислениями в удобных точках, взятых внутри этих интервалов, или в соответствии с правилом расстановки знаков и выписывается ответ. В частности, если P(x) и Q(x) не|
содержат множителей вида |
|
, где |
|
, или общих множителей (x-d) в одинаковых |
|
|
степенях, то достаточно определить знак |
|
в любом интервале, а в остальных интервалах |
|||
знаки будут чередоваться.
![]()
Internet-school | Школа "Абитуриент" | Учебное пособие | Краткий справочник по математике | Наши адреса