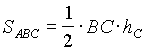 (1), где
(1), где § 2.
ИСПОЛЬЗОВАНИЕ ФОРМУЛ ПЛОЩАДИ МНОГОУГОЛЬНИКОВСвойство 1 - не единственный, хотя и важный инструмент для решения задач на площади. Конечно, надо знать и уметь использовать формулы площадей фигур. Например, формула площади трапеции, доказанная в примере 2, позволяет легко решить одну из задач для самостоятельного решения.
Треугольник является простейшей геометрической фигурой. Каждый многоугольник можно разрезать на треугольники. Поэтому при решении задач на площади многоугольников часто помогают известные вам формулы площади треугольника.
Вот, например, основная формула площади треугольника: 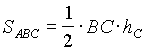 (1), где
(1), где ![]() - длина высоты, опущенной из точки С на прямую AB. Что она может нам дать? Из этой формулы срезу следует такие свойства площади:
- длина высоты, опущенной из точки С на прямую AB. Что она может нам дать? Из этой формулы срезу следует такие свойства площади:
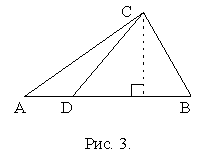
Свойство 2. Для любого треугольника ABC и любой точки D отрезка AB имеет место равенство SACD: SBCD=AD:BD (см. рис.3). В частности, любая медиана треугольника делит его площадь пополам.
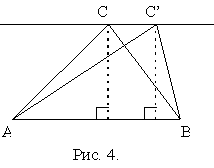
Свойство 3. При фиксированном основании AB для любых двух точек C и С', лежащих на прямой, параллельной AB, площади треугольников ACB и AC'B равны (см. рис.4).
Доказательство. Поскольку СС'| | AB, то длины высот, опущенных на AB из С и С', равны. Применив теперь формулу (1), получаем, что 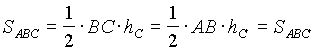 . Отметим еще
. Отметим еще
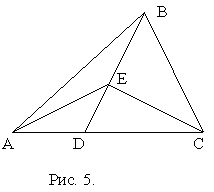
Свойство 4. Пусть в треугольнике ABC точка D лежит на отрезке AC, точка E лежит на отрезке BD. Тогда SABE : SCBE = AD : DC.
Доказательство.
Пусть AD : DC=Пример 3. Пусть
ABCD - выпуклый четырехугольник и О - точка пересечения его диагоналей . Доказать, что площади треугольников ABO и CDO равны тогда и только тогда, когда BC | | AD.Замечание.
Обратите внимание, что в этом примере (как и в других, где в утверждении встречается выражение "тогда и только тогда") нужно доказать два факта: (а) если SABC=SCDO, то BC | | AD; (б) если BC | | AD, то SABC=SCDO.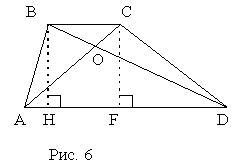
Решение примера
3. Поскольку SACD=SACD+SCDO; SABD=SACD+SABC, то площади треугольников ABO и CDO равны тогда и только тогда, когда равны площади треугольников ABD и ACD.Допустим, что
SABC=SACD. Так как эти треугольники имеют общее основание AD , то из формулы (1) следует, что длины перпендикуляров BH и CF (см. рис.6) к прямой AD , опущенных из точек B и C, равны. Но тогда четырехугольник BCFH является параллелограммом (BH=CF, BH | | CF) и, следовательно, BC | | AD.Допустим теперь, что
BC | | AD. По свойству 3, примененному к треугольникам ABD и ACD, получаем SABC=SACD.Пример 4.
Доказать, что в равнобедренном треугольнике ABC (AB=BC) сумма расстояний от любой точки D отрезка AC до сторон AB и BC одна и та же.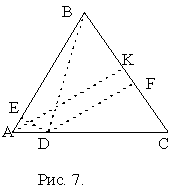
Доказательство. Достаточно показать, что для любой точки D отрезка AC сумма расстояний DE+DF от точки D до AB и BC равна расстоянию AK от вершины А до BC.
Посчитаем площадь треугольника
ABC двумя способами. По формуле (1)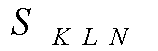 . С другой стороны,
. С другой стороны, 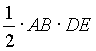 =
= 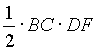 . Сравнивая эти два выражения площади треугольника ABC и учитывая, что AB=BC, получаем:
. Сравнивая эти два выражения площади треугольника ABC и учитывая, что AB=BC, получаем:
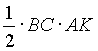 =
=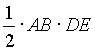 +
+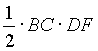 =
=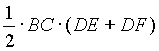 .
.
Отсюда сразу следует, что
AK=DE+DF, что и требовалось.Столь же важной, как и формула (1), является следующая:
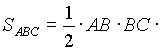 sin РBAC (2)
sin РBAC (2)
Они позволяют сравнивать площади треугольников, имеющих общий угол.
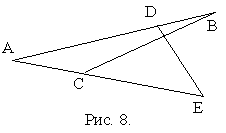
Свойство 5. Пусть на одной из сторон угла с вершиной A лежат точки B и D, а на другой - точки C и E. Тогда ![]()
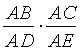 .
.
Доказательство.
Согласно формуле (2) имеем![]() =
=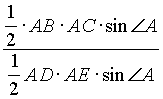 =
=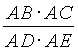 =
=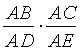 .
.
Свойство доказано.
Несмотря на свою простоту, почти очевидность, свойства 2-5 иногда существенно облегчают решение задач.
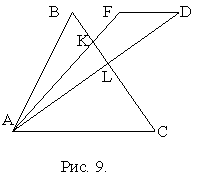
Пример 5. Дан треугольник
ABC. Точка L делит сторону BC пополам. Точка К делит пополам отрезок BL. Из вершины A через точки K и L проведены лучи и не них отложены вне треугольника отрезки LD и KF, причем LD=AL, KF=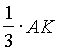 . Найти отношение площадей треугольника ABC и четырехугольника KLDF.
. Найти отношение площадей треугольника ABC и четырехугольника KLDF.
Решение.
В треугольниках ABC и AKL высоты, опущенные из точки А, совпадают. По условию задачи KL=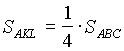 .
.
По свойству 3, 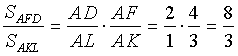
Согласно свойству 1, ![]()
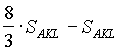 =
= 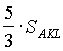 =
= 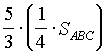 =
= 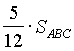
Ответ: ![]()
Кроме (1) и (2), вы знаете из школьного курса следующие формулы площади треугольника:
![]() =
=![]() ; (3)
; (3)
![]() =
=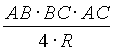 ; (4)
; (4)
![]() =
=![]() ; (5)
; (5)
Здесь через
p обозначается полупериметр треугольника ABC, а через r и R - радиусы его вписанной и описанной окружностей.Эти формулы тоже могут пригодиться. Например, формула (3) используется при решении примера 11 в § 4 и задачи 12 вашего задания.
Internet-school | Условия задач | Методические указания | Наши адреса | Правила оформления рукописей