При решении задач, связанных с площадями фигур, часто помогает следующий простой факт.

Свойство 1. Площадь плоской фигуры, разрезанной на несколько частей, равна сумме площадей этих частей.

Опираясь на это свойство, в учебнике геометрии из формулы площади прямоугольника выводятся формулы площадей параллелограмма, треугольника и трапеции. Приведем еще примеры применения свойства 1.

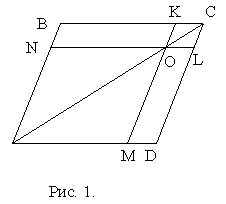
Пример 1. Через точку, взятую на диагонали AC параллелограмма ABCD, проведены прямые параллельные его сторонам. Данный параллелограмм делится этими прямыми на четыре параллелограмма. Два из них пересекаются диагональю AC. Докажите, что два другие равновелики (т.е. имеют одинаковые площади, хотя не обязательно равны).

Замечание. Перед тем как прочитать решение этого и следующих примеров, попробуйте решить их сами.

Доказательство. Поскольку диагональ параллелограмма делит его на два равных треугольника, то S_ABC=S_ADC, S_ANO=S_AMO, S_CKO=S_CLO. Следовательно, S_OLDM=S_ADC-S_AMO-S_CLO=S_ABC-S_ANO-S_CKO=S_BKON, что и требовалось.

Пример 2. Доказать, что площадь трапеции равна произведению длины одной из ее боковых сторон на длину перпендикуляра к этой стороне, опущенного на нее из середины другой стороны.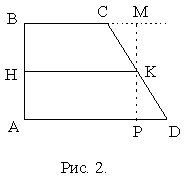

Доказательство. Рассмотрим трапецию ABCD, где BC | | AD, . Пусть K - середина CD и . Проведем через точку K прямую, параллельную AB. Обозначим через M и P точки пересечения этой прямой с прямыми BC и AD соответственно.

Так как BC | | AD по условию и MP | | AB по построению, то ABMP - параллелограмм и , так как KH - его высота, ведь . Поскольку BM=AP (как противоположные стороны параллелограмма), BC<AD, а точка K принадлежит отрезку MP, то . Это означает, что точка M лежит на продолжении BC, а точка P - внутри отрезка AD, т.е. так, как и нарисовано на рис. 2.

Треугольники CMK и KPD равны (CK=KD, , ) Следовательно, S_ABCD=S_ABMP - S_CMK+S_KPD=S_ABMP=, что и требовалось.

Internet-school | Условия задач | Методические указания | Наши адреса | Правила оформления рукописей