Районные олимпиады по математике 1997-1998 г 10 класс

Задания

  1. Можно ли какое-нибудь простое число представить в виде суммы нескольких последовательных нечетных чисел?

  2. Известно, что a+b+c<0 и что уравнение ax2+bx+c=0 не имеет действительных корней. Определите знак с.

  3. На биссектрисе прямого угла взята точка Р. Через нее проводится произвольная прямая, высекающая на сторонах угла отрезки длины а и b. Будет ли величина 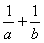зависеть от этой прямой.

  4. Доказать, что если

а1 - 3а2+2а3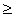0

а2 - 3а3+2а4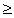0

. . . . . . .

аn-2 - 3an-1 + 2an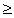0

an-1 - 3an + 2a1 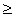0

an - 3a1 + 2a2 > 0, то a1= a2=. . . = an.

  1. Диагонали AC и BD выпуклого четырехугольника ABCD пересекаются в точке О. Точки М, N и К соответственно являются серединами отрезков AB, BC и ОС. Найдите отношения площадей четырехугольников ABCD и MBNK, если BО:OD=2:1995.

Internet-school | Математические соревнования | Олимпиады | Ответы и указания к решению