Задачи Параметры Ответы Теория Решение

Д Пример 1. Наиболее известным примером испытаний Бернулли является последовательное бросание правильной симметричной монеты; здесь p=q=1/2. Если отказаться от условия симметричности монеты, то мы по-прежнему считаем последовательные испытания независимыми и вновь получаем испытания Бернулли, в которых вероятность успеха может быть произвольной. Г

Д Пример 2. В примере бросания правильной кости испытание Бернулли возникает, если мы будем описывать результат как А и не А (например, “успех” - если выпала цифра 6 и “неудача” в противном случае). Здесь p=1/6, q=5/6.

Если кость несимметрична, то соответствующие вероятности p и q могут измениться. Г

Д Пример 3. Стрелок совершает пять выстрелов по мишени, причем все выстрелы производятся практически в одних и тех же условиях. При этом попадание в яблоко мишени рассматривается как “успех” испытания, и число успехов за 5 испытаний может меняться от 0 до 5.Г

Д Пример 4. Из урны, содержащей N шаров, среди которых М - белых и N-M - черных, последовательно извлекается шар, фиксируется его цвет, и затем шар возвращается обратно. Ясно, что каждое такое извлечение есть испытание Бернулли с .Г

Д Пример 5. ( задача о снабжении энергией). Пусть n (n=10) рабочих должны время от времени использовать электроэнергию. Приближенно можно считать, что в течение любого заданного промежутка времени каждому рабочему с одной и той же вероятностью требуется единица энергии. Пусть рабочие действуют независимо друг от друга, тогда обозначим вероятность того, что одновременно ровно k рабочим потребуется энергия через Р_n(k).

Если каждый рабочий использует электроэнергию в среднем 12 минут в час, то следует положить p=1/5. Тогда вероятность того, что не менее S рабочим (0 Ј S Ј 10) одновременно потребуется электроэнергия, равна и, например, при s=7:

.

Иначе говоря, если снабжение рассчитано на шесть единиц энергии, то вероятность перегрузки равна 0,00086 и приблизительно одной минуте из 20 часов работы. Г

Д Пример 6 (проверка сывороток или вакцин). Предположим, что нормальная частота заболеваний определенной болезнью среди крупного рогатого скота составляет 25%. Для проверки новой вакцины n животным делают прививки. Разберем вопрос об оценке результата эксперимента.

Если вакцина абсолютно недейственна, вероятность иметь ровно k здоровых среди n подвергнувшихся прививкам Р_n(k) ( в этом случае вероятность успеха р есть вероятность того, что животное здорово, и равно 0,75 ).

Для k=n=10 P₁₀(10)=p¹⁰=0,75^10» 0,056.

Для k=n=12 P₁₂(12)» 0,032.

Таким образом, отсутствие заболеваний среди десяти или двенадцати животных можно рассматривать как подтверждение эффективности вакцины. Отметим, что вероятность иметь не более одного заболевшего из 17 животных: P{m _17і 16}= 1-p{ m ₁₇=16} -p{ m ₁₇=17} » 0,050.

Следовательно, заболевание одного животного среди 17 - есть более сильное подтверждение эффективности вакцины, чем отсутствие болезни в партии из 10 животных. Г

Д Пример 7. Для стрелка, выполняющего упражнения в тире, вероятность попасть в “яблочко” равна р=1/4. Спортсмен сделал 5 выстрелов. Найти вероятность событий: А - ровно одно попадание; В - ровно два попадания; С - хотя бы одно попадание; D - не менее трех попаданий.

Решение. Моделью настоящего опыта является схема Бернулли с р=1/4, q=3/4.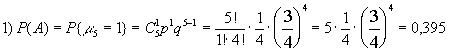

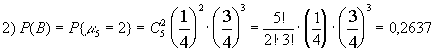
3) Событие С представляет собой сумму событий {m ₅=k} при 1Ј k Ј 5 и тогда по теореме сложения:

Но, с другой стороны, , то есть событие, заключающееся в том, что стрелок не попал ни разу, есть событие {m ₅=0}.

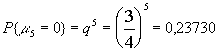. Следовательно: Р(С)=1-Р()=0,7627.

4) , следовательно:

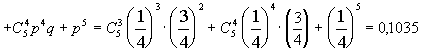.Г

Д Пример 8. Большая партия изделий содержит один процент брака. Каков должен быть объем случайной выборки, чтобы вероятность встретить в ней хотя бы одно бракованное изделие была не менее 0,95.

Решение. В данном случае рассматривается схема Бернулли с р=0,01. Успехом считается появление брака. Требуется найти такое n, что

Р{m _{n і} 1}> 0,95.
Имеем Р{m _n і 1}= 1-P{m _n=0}=1-(1-p)ⁿ і 0,95; р=0,01, откуда .Г

Д Пример 9. Имеется партия изделий. Каждое из изделий партии независимо от других может оказаться дефектным с вероятностью р. Из партии произвольным образом выбираются 15 изделий и эти изделия проверяются на годность. Если число дефектных изделий в выборке не более двух, то партию принимают, в противном случае - подвергают сплошному контролю. Какова вероятность того, что партия, для которой р=0,2 , будет принята ?

Решение. Искомая вероятность - есть вероятность не более 2 успехов в 15 испытаниях схемы Бернулли с р=0,2.

.Г

Д Пример 10. Для данного баскетболиста вероятность забросить мяч в корзину при броске - 0,4. Произведено 10 бросков. Найти наивероятнейшее число попаданий и соответствующую вероятность.

Решение. np-q < m₀ < (n+1)p; 3,6 < m₀ < 4,4; m₀=4.

.Г

Задачи Параметры Ответы Теория Решение

Случайные события