Примеры задач по сложным событиям.

Задачи Параметры Ответы Теория Решение

Д Пример 1. Турист из пункта А в пункт В может попасть двумя дорогами. Обозначим события: Е₁ - турист пошел первой дорогой, Е₂ - турист пошел второй дорогой. Из пункта В в пункт С ведут три дороги. Обозначим события: D₁ - турист пошел первой дорогой, D₂ - турист пошел второй дорогой, D₃ - турист пошел третьей дорогой. Если событие F₁ - турист от пункта А до пункта В выбрал дорогу наугад, а от пункта В до пункта С пошел третьей дорогой, то F₁=(E₁+E₂)D₃. Если событие F₂ - турист от пункта А до пункта В пошел не первой дорогой, а от пункта В до пункта С не третьей дорогой, то F₂=E₂(D₁+D₂). Если событие F₃ - турист дошел от пункта А до пункта С, то F₃=(E₁+E₂) (D₁+D₂+D₃).Г

Д Пример 2. Из первых десяти натуральных чисел наугад выбирают одно. Найти вероятность того, что выбранное число четное или кратное пяти.

Пусть событие А - выбранное число четное, событие В - выбранное число кратно пяти. Тогда событие А+В - выбранное число четное или кратно пяти, событие АВ - выбранное число четное и кратно пяти. По классическому определению вероятности Р(А)=0,5 Р(В)=0,2 и Р(АВ)=0,1. Следовательно, по теореме сложения Р(А+В)=0,5+0,2-0,1=0,6.

Заметим, что в этом простом опыте вероятность события А+В можно легко найти непосредственно по классическому определению вероятности, так как: А+В={2; 4; 5; 6; 8; 10 } для пространства элементарных событий W ={1; 2; 3; 4; 5; 6; 7; 8; 9; 10}.Г

Д Пример 3. В ящике содержатся 10 одинаковых по форме и весу шаров. Среди этих шаров 6 белых и 4 черных. Наугад вынимают последовательно два шара. Найти вероятность того, что вынутые шары белые.

Пусть событие А - первый вынутый шар белый; событие В -второй вынутый шар белый. По классическому определению вероятности Р(А)=0,6 Р(В/А)=5/9. Следовательно, Р(АВ)=Р(А)Р(В/А)=1/3.Г

Д Пример 4. Брошены 3 игральные кости. Найти вероятность выпадения хотя бы одной “шестерки” на верхних гранях костей.

Обозначим событие А - выпала хотя бы одна “шестерка”, тогда событие - не выпало ни одной “шестерки”. По теореме умножения

Р()=(5/6)³. Тогда Р(А)=1-Р()=1-(5/6)³.

Пусть пространство элементарных событий W представлено в виде W =Н₁+Н₂+Н₃+...+Н_n+..., где Н_k- попарно несовместные события, которые часто называют гипотезами.

Если событие Р(Н_k)>0 при k=1,2,..., то для любого события А справедливы: формула полной вероятности и формулы Байеса 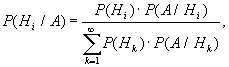где i=1,2,...Г

Д Пример 5. В первом ящике лежат 1 белый шар и 4 черных, а во втором ящике 1 белый и 7 черных. В первый ящик добавляются два шара, случайно выбранных из второго ящика. Найти вероятность того, что шар, выбранный наугад из пополненного первого ящика, будет черным.

Пусть А- событие, вероятность которого требуется найти. Рассмотрим события: Н₁- в первый ящик добавили два черных шара; Н₂ - в первый ящик добавили один белый и один черный шар. Тогда: . Следовательно, по формуле полной вероятности . Г

Д Пример 6. В тур слете участвуют 70% девятиклассников и 30% десятиклассников. Среди девятиклассников 60% мальчиков, а среди десятиклассников 40% мальчиков. Все мальчики по очереди дежурят у костра, сменяясь каждый день. Найти вероятность того, что в случайно выбранный день у костра дежурит девятиклассник.

Пусть событие А - у костра дежурит мальчик, событие Н₁ - у костра дежурит кто-то из девятиклассников; событие Н₂ - у костра дежурит кто-то из десятиклассников. Тогда Р(Н₁)=0,7; Р(Н₂)=0,3; Р(А/Н₁)=0,6; Р(А/Н₂)=0,4.

Следовательно, по формуле Байеса .Г

Задачи Параметры Ответы Теория Решение

Случайные события