примеры к данной теме

ВЫЧЕТЫ И ИХ ВЫЧИСЛЕНИЯ

Лемма. Если функция F(z) регулярна в кольце {z:r<|z–a|<R}, то интеграл

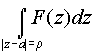, r<r <R, не зависит от r.

Пусть z=a – изолированная особая точка однозначного характера функции f (z). Вычетом функции f (z) в точке z=a (а ) называется величина

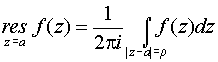
(r >0 – любое достаточно малое число). При а=

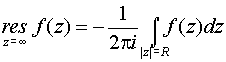
(R>0 – любое достаточно большое число). Направление интегрирования выбрано так, чтобы внутренность круга осталась слева.

Независимость интегралов в последних формулах от r и R соответственно следует из леммы.

Пусть функция f (z) регулярна в некоторой проколотой окрестности конечной или бесконечно удаленной точки z=a. Тогда вычет в точке а равен деленному на 2pi интегралу от f (z) по границе любой достаточно малой окрестности точки а, ориентированной в положительном направлении.

Очевидно, что , если а (а) – точка регулярности функции f (z). Однако вычет в бесконечно удаленной точке может оказаться отличным от нуля и для функции, регулярной в ¥ .

Например, для функции

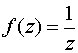
имеем

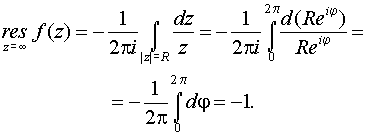
Основные формулы для нахождения вычетов:

1. Если а – устранимая особая точка для функции f (z), то

.

2. Если а – полюс первого порядка функции f (z), то

В частности, если

,

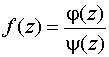где j(z) и y(z) – регулярные в точке а функции, причем j(а) 0, y(а)0, y¢(а) 0, то точка а является простым полюсом функции f (z) и

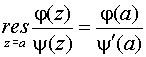3. Если точка а – полюс порядка т 1 для функции f (z), то

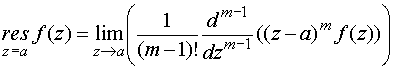В частности, если 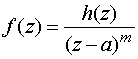, h(z) – регулярна в точке а, h(а)0, то справедлива формула

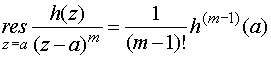4. Если f (z) регулярна в точке z=, то

где .

5. Если функция f (z) представима в виде

,

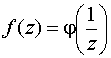где функция 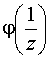регулярна в точке x =0, то

Теорема. Если z=a (а ) – изолированная особая точка однозначного характера функции f (z), то

где с_–1 – коэффициент при в ряде Лорана функции f (z) в окрестности точки z=a и

,

где с_-1 – коэффициент при в ряде Лорана функции f (z) в окрестности точки z=.