
Задание 28. Найти изображения функций:
а) f (t)=cos2t (здесь и далее считается, что f (t)=0 при t<0);
б) f (t)=chаt× sinbt; в) f (t)=e–4b× sin3t× cos2t.
Решение:
а) Воспользуемся формулой
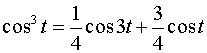 .
.
Используя далее свойства линейности, подобия и формулу (5) из таблицы изображений, имеем
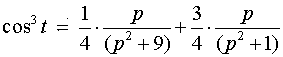 ,
,
т. е.
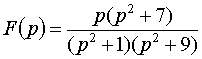 .
.
б) Поскольку
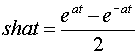 ,
,
то
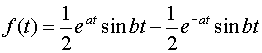 .
.
Применяя свойства линейности и формулу (8) из таблицы изображений, получим
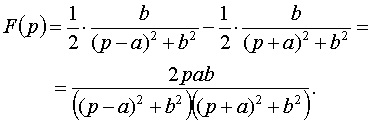
в) Преобразуя произведение тригонометрических функций в сумму, имеем
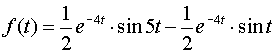 .
.
Далее, аналогично примеру б), получим
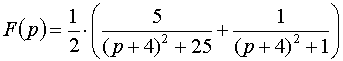 .
.
Задание 29.Найти изображение функции, заданной графически.
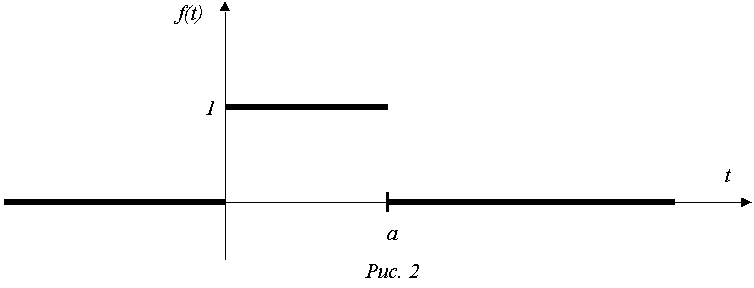
Решение. Воспользовавшись определением единичной функции Хевисайда
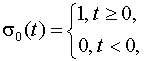
запишем уравнение оригинала, заданного рис. 2, в виде
![]() .
.
Применяя теорему запаздывания имеем
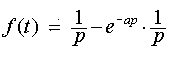 ,
,
итак

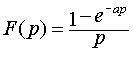 .
.