Будем рассматривать уравнения вида P(x) = 0,
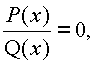
где
P(x) иQ
(x) – многочлены, а также уравнения вида f(x) = g(x), где f(x) и g(x) – рациональные выражения.2.3
. Рациональные уравнения|
Будем рассматривать уравнения вида P(x) = 0, |
|
где P(x) и |
|
Q (x) – многочлены, а также уравнения вида f(x) = g(x), где f(x) и g(x) – рациональные выражения. |
||
@ Полезными являются следующие утверждения:
1. Если x = a – корень многочлена P(x), то P(x) делится без остатка на двучлен x – a.
2. Пусть все коэффициенты многочлена P(x) – целые числа, причем старший коэффициент равен 1. Если такой многочлен имеет своим корнем рациональное число, то это число целое.
3. Пусть все коэффициенты многочлена P(x) = a0xn + a1xn-1 + ... + an – целые числа. Если корнем многочлена является целое число b, то b – делитель свободного члена an.
При решении многих уравнений основными являются два метода: разложение на множители и введение новых (вспомогательных) переменных.